La créature sera-t-elle bientôt au-dessus de son créateur ? C'est le futur que laisse entrevoir AlphaGeometry, développée par Google DeepMind. Une IA de tous les records, capable de résoudre des problèmes géométriques complexes et qui présage d'une petite révolution au sein des modèles d'IA généralistes.
au sommaire
DeepMind vient de frapper un grand coup : le laboratoire d'IA de GoogleGoogle a annoncé en janvier avoir développé AlphaGeometry, une intelligence artificielle révolutionnaire capable de rivaliser avec les médaillés d'or des Olympiades internationales dans la résolution de problèmes de géométrie. Si cela ne vous parle pas, sachez que les médailles Fields - Terence Tao, Maryam Mirzakhani et Grigori Perelman - ont tous les trois été médaillés d'or lors de cette compétition annuelleannuelle de mathématiques qui fait s'affronter les meilleurs collégiens et lycéens du monde. Or, AlphaGeometry a résolu avec succès 25 des 30 problèmes de géométrie de l'Olympiade, se rapprochant ainsi du score moyen des médaillés d'or humains. C'est 15 de plus que son prédécesseur. Mais comment les scientifiques de DeepMind ont-ils accompli un tel exploit ?
L'approche neuro-symbolique, la petite révolution de l'IA
AlphaGeometry est le fruit d'une approche neuro-symbolique, combinant un modèle de langage neuronal (MLN) et un moteur de déduction symbolique (MDS).
Les MLN sont des réseaux de neuronesneurones artificiels entraînés sur de vastes ensembles de données textuelles. Ils sont capables d'apprendre et de reconnaître des schémas et des structures dans les données textuelles, ce qui leur permet de générer du texte cohérent et de comprendre le langage naturel. Les MDS sont, pour leur part, particulièrement efficaces pour traiter des problèmes qui nécessitent une manipulation formelle des symboles et des règles logiques.
L'approche neuro-symbolique permet de faire travailler ces deux composantes en tandem : dans le cadre d'AlphaGeometry, le MLN prédit des constructionsconstructions géométriques potentiellement utiles, puis le MDS utilise ces prédictions pour guider la résolution du problème. Cette combinaison offre à l'IA les capacités intuitives des réseaux de neurones et la rigueur logique des moteurs de déduction symbolique, ce qui lui permet de résoudre efficacement des problèmes de géométrie complexes.
Pour surmonter le manque de problèmes mathématiques de niveau Olympiades qui auraient dû servir de données d'entraînement à AlphaGeometry, les chercheurs ont développé une méthode innovante de génération de données synthétiques à grande échelle, permettant au génial bébé de DeepMind de s'entraîner sur un ensemble de 100 millions d'exemples uniques.
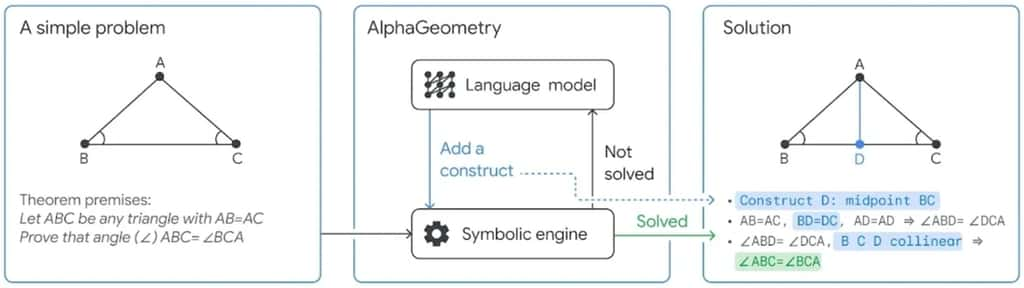
« AlphaGeometry résout un problème simple : étant donné le diagramme du problème et les prémisses du théorème (à gauche), AlphaGeometry (au milieu) utilise d'abord son MDS pour déduire de nouveaux énoncés sur le diagramme jusqu'à ce que la solution soit trouvée ou que les nouveaux énoncés soient épuisés. Si aucune solution n'est trouvée, le MLN ajoute une construction potentiellement utile (bleu), ouvrant de nouvelles voies de déduction pour le MDS. Cette boucle continue jusqu'à ce qu'une solution soit trouvée (à droite). Dans cet exemple, une seule construction est nécessaire. » © DeepMind
Mission : repousser les frontières de la connaissance
Cette réalisation marque une avancée significative dans le développement de systèmes d'IA capables de raisonner et de résoudre des problèmes mathématiques complexes, rapportent les chercheurs de DeepMind dans un article paru dans Nature en février dernier. Bien que présentant des résultats impressionnants, AlphaGeometry se heurte tout de même à quelques défis, notamment celui de s'adapter à des scénarios mathématiques de plus en plus complexes et à mobiliser ses compétences dans des domaines mathématiques autres que la géométrie.
Malgré tout, cette avancée ouvre la voie à d'extraordinaires possibilités dans les domaines des mathématiques, des sciences et de l'IA. Ses créateurs ne cachent d'ailleurs pas leur ambition : « Notre objectif à long terme reste de construire des IA capables de transférer leurs compétences et leurs connaissances dans tous les domaines mathématiques en développant la résolution de problèmes et le raisonnement sophistiqués dont dépendront les systèmes d'IA généraux », assènent Trieu Trinh et Thang Luong, les responsables du projet dans un communiqué.
Le ton est donné : autrement dit, les systèmes d'IA développés par DeepMind doivent acquérir des capacités de résolution de problèmes sophistiquées et de raisonnement, ce qui implique la capacité à identifier des schémas, à formuler des hypothèses, à déduire des conclusions et à prendre des décisions logiques dans des contextes variés. Le tout en « repoussant les frontières de la connaissance humaine ». Très ambitieux, mais peut-être pas impossible.