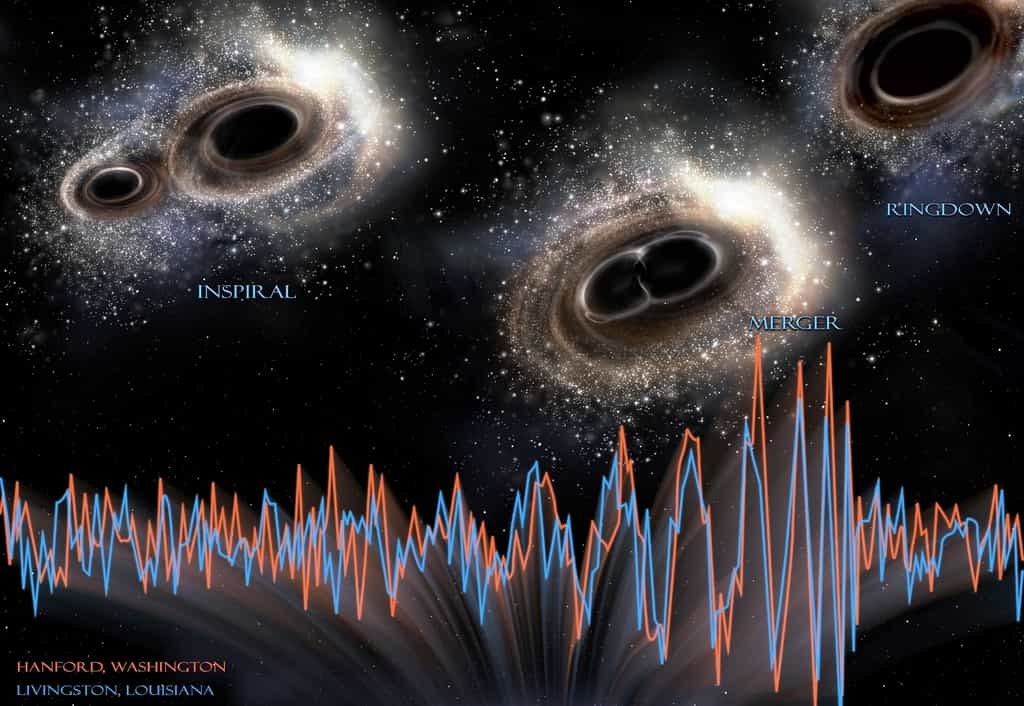
Les modes quasi-normaux des trous noirs sont des modes de vibrations fondamentaux et caractéristiques de l'horizon des évènements des trous noirs. Ils conduisent à l'émission d'ondes gravitationnelles au fur et à mesure de l'amortissement de ces vibrations qui font prendre ou reprendre à un trou noir sa forme initiale. On cherche à mettre en évidence ces modes dans le spectre des ondes gravitationnelles, produits notamment lorsque deux trous noirs stellaires entrent en collision et fusionnent pour donner un nouveau trou noir.
au sommaire
Pour comprendre un peu mieux de quoi il en retourne en ce qui concerne les modes quasi-normaux des trous noirs et pour rendre compte de la découverte de cette propriété fondamentale des trous noirs, il est bon de se plonger un peu dans l'histoire de la théorie des trous noirs au XXe siècle, alors que l'on commençait vraiment à comprendre les propriétés mathématiques des solutions des équations de la relativité générale décrivant l'espace-temps de la métrique de Schwarzschild pour un trou noir statique, et de Kerr pour un trou noir stationnaire en rotation.
Comme EinsteinEinstein et d'autres, le physicienphysicien John Wheeler était initialement sceptique quant à l'existence de ce qu'il a lui-même appelé un trou noir, en 1967, et qui était impliqué par la solution de Schwarzschild. Il changea d'avis au début des années 1960 et avec ses collaborateurs, il se joignit à l'école britannique menée par un ancien thésard de Paul DiracPaul Dirac, Denis Sciama, et ses élèves (Roger PenroseRoger Penrose et Stephen Hawking), ainsi qu'à l'école russe menée par Yakov Zeldovitch et Igor Novikov, pour explorer la théorie des trous noirs pendant la période allant de 1963 à 1973 environ, période appelée depuis l'âge d'or de la théorie des trous noirs. On peut la faire débuter avec la découverte de la solution de Kerr décrivant un trou noir en rotation et la faire finir avec la découverte du rayonnement des trous noirs par Hawking.

Des trous noirs qui vibrent quand ils entrent en collision
Les physiciens et mathématiciensmathématiciens relativistes vont alors définir les trous noirs uniquement comme des objets occupant une région fermée de l'espace-temps dont rien ne peut sortir du fait du caractère fini de la vitesse de la lumière : l'horizon des évènements - c'est la présence d'un tel horizon, et rien d'autre, qui définit un trou noir, pas même la présence d'une singularité avec densité et courbure infinie de l'espace-temps en son centre qui est, de plus, douteuse à cause des effets quantiques. Ils vont montrer qu'il n'existe alors qu'une famille de solutions nécessairement rigoureusement exactes des équations d'Einstein décrivant un trou noir. Cette famille ne dépend uniquement que de la masse, du moment cinétique et, éventuellement, des charges électriques, voire magnétiques des particules absorbées et de rien d'autre. C'est le théorèmethéorème de l'unicité des trous noirs, plus souvent connu comme le théorème de la calvitiecalvitie pour les trous noirs, en anglais le célèbre « no-hair theorem ».
Concrètement, dans le royaume de l'astrophysiqueastrophysique où les étoilesétoiles tournent toutes et où l'on s'attend naturellement à la formation de trous noirs à partir de ces étoiles en fin de vie lorsqu'elles sont suffisamment massives et que leur cœur s'effondre en donnant des supernovaesupernovae, les plus simples sont sans rotation et possèdent uniquement une masse, les trous noirs de Schwarzschild ; et les plus réalistes sont aussi en rotation, les trous noirs de Kerrtrous noirs de Kerr.
En théorie, ils ne gardent pas la mémoire des caractéristiques différentes d'objets de même masse et de même moment cinétique qui tomberaient dans ces régions particulières de l'espace-temps. Ils oublient en particulier des nombres quantiquesnombres quantiques normalement conservés associés aux baryonsbaryons et aux leptonsleptons - ce qui joue peut-être un rôle encore mystérieux dans la solution de l’énigme de l’absence d’antimatière en cosmologiecosmologie.
La surface de l'horizon des évènements d'un trou noir, de Schwarzschild ou de Kerr, est parfaitement lisse, sphérique (d'où le lien avec le terme de calvitie) mais elle se déforme temporairement en devenant bosselée lorsqu'un trou noir absorbe un objet, par exemple un astéroïdeastéroïde, ou lors d'une collision avec un autre trou noir.

Des modes quasi-normaux caractéristiques des trous noirs
Cette dernière situation est très intéressante car la collision et la fusionfusion de deux trous noirs en forment un autre. Ce trou noir nouvellement formé, là non plus, n'a pas un horizon régulier des évènements. Les équations d'Einstein sont alors formelles, cela ne peut durer et, très rapidement, la surface de l'horizon vibre comme le ferait une cloche sous l'effet d'un coup. Il existe alors, ce que l'on appelle d'ailleurs dans les deux cas, des modes quasi-normaux pour ces vibrationsvibrations qui vont s'amortir, sous l'effet de l'émissionémission d'ondes gravitationnellesondes gravitationnelles dans les premiers cas, et avec des émissions sonores pour une cloche. L'effet d'amortissement va faire prendre au trou noir, après une fusion, la forme exacte décrite par la fameuse métrique de Kerr pour un trou noir sans charges en rotation.
Comme ces modes quasi-normaux ont des fréquencesfréquences déterminées par la théorie des trous noirs, fixés par la masse et le spinspin du trou noir final, faire leur découverte dans le spectrespectre des ondes gravitationnelles serait une preuve très convaincante de l'existence d'un horizon des évènements et donc, de l'existence des trous noirs... mais à condition que les fréquences trouvées (d'autres astresastres compacts avec des modes quasi-normaux sans horizon des évènements sont possibles) soient précisément celles déduites des solutions perturbées décrivant des trous noirs.
Rappelons pour la suite de cet article que les équations de la théorie de la relativité généralerelativité générale sont non-linaires. Elles sont donc beaucoup plus difficiles à résoudre que dans le cas des équations linéaires et nécessitent parfois l'usage de simulations numériquessimulations numériques sur ordinateurordinateur. Ce n'est pas un cas unique, les équations de Navier-Stokes en mécanique des fluides, non-linéaires elles aussi, peuvent par exemple être utilisées analytiquement pour décrire le mouvementmouvement de petites vaguesvagues à la surface de l'eau. Peut alors s'appliquer ce que l'on appelle la méthode des perturbations, méthode que l'on a aussi appliquée en régime linéaire pour décrire la façon dont les trous noirs se comportent lorsqu'ils subissent des effets de faibles intensités. Mais dans d'autres situations, l'usage de l'ordinateur devient nécessaire.
L'étude des modes quasi-normaux est un sujet de recherche important car des alternatives aux trous noirs, comme les gravastars, ont été proposées pour rendre compte des objets observés en astrophysique, comme Sgr A* ou M 87*, qui semblent jusqu'à un certain point se comporter comme des trous noirs.

C'est précisément, en partie, pour tenter de mettre fin au débat quant à l'existence réelle des trous noirs que les projets de détecteurs d'ondes gravitationnelles que sont Ligo, Virgo et eLisa ont été conçus et lancés.
La découverte de la première source d'ondes gravitationnelles qui a frappé la Terre le 14 septembre 2015 a donc fait grand bruit. GW150914 correspondait à une collision suivie d'une fusion de deux trous noirs stellairestrous noirs stellaires ayant dégagé en moins d'une seconde 50 fois plus d'énergieénergie que toutes les étoiles de l'universunivers observable, fût-elle sous forme électromagnétique, elle aurait paru dans notre ciel plus lumineuse que la Pleine LunePleine Lune, bien que cette source soit distante de 1,3 milliard d'années-lumièreannées-lumière environ.
Depuis lors, plusieurs dizaines de sources d'ondes gravitationnelles avaient été identifiées et les physiciens avaient bon espoir qu'avec l'essor de l'astronomie gravitationnelle et la montée en sensibilité des instruments, on finirait par identifier, puis mesurer de plus en plus finement les modes quasi-normaux des trous noirs.
En 2019, une nouvelle analyse des données enregistrées concernant GW150914, le signal qui est, à ce jour, le plus clair avec un rapport signal/bruit étant le plus élevé comme disent les astrophysiciensastrophysiciens dans leur jargon, est très encourageante à ce sujet.
Deux articles sur des modes quasi-normaux probablement détectés ont été déposés sur arXiv, cosignés par Matthew Giesler, Maximiliano Isi, Mark Scheel et le célèbre astrophysicien relativiste Saul Teukolsky, bien connu pour ses simulations numériques sur ordinateurs concernant la physiquephysique des trous noirs et sa découverte technique d'une méthode de séparationséparation des variables pour résoudre analytiquement des équations décrivant des perturbations de la métrique de l'espace-temps des trous noirs de Kerr.
Dans cette vidéo, Aurélien Barrau explique pourquoi la détection des modes quasi-normaux des trous noirs est potentiellement très importante pour découvrir une nouvelle physique, y compris celle relevant d'une théorie quantique de la gravitation. © Aurélien Barrau