Les sangakus sont de petites tablettes mathématiques en bois, pendues dans des sanctuaires shinto, et parfois dans des temples bouddhistes, au Japon. Elles datent de l’époque Edo (1603 – 1868), qui a précédé l’ère Meiji, pendant laquelle le Japon s’est occidentalisé. En voici une, contenant onze énigmes.
au sommaire
Ces petits tableaux peints représentent des figures mathématiques composées de droites et de cercles. Les commentaires échappent à ceux qui ne comprennent pas la langue, mais le mathématicien y verra un défi à relever, un problème à résoudre.
Par exemple, dans le suivant découvert par Hidetoshi Fukagawa, un professeur de mathématiques japonais contemporain, il s'agit de trouver le rapport des rayons des cercles bleus sachant que les triangles sont équilatéraux.
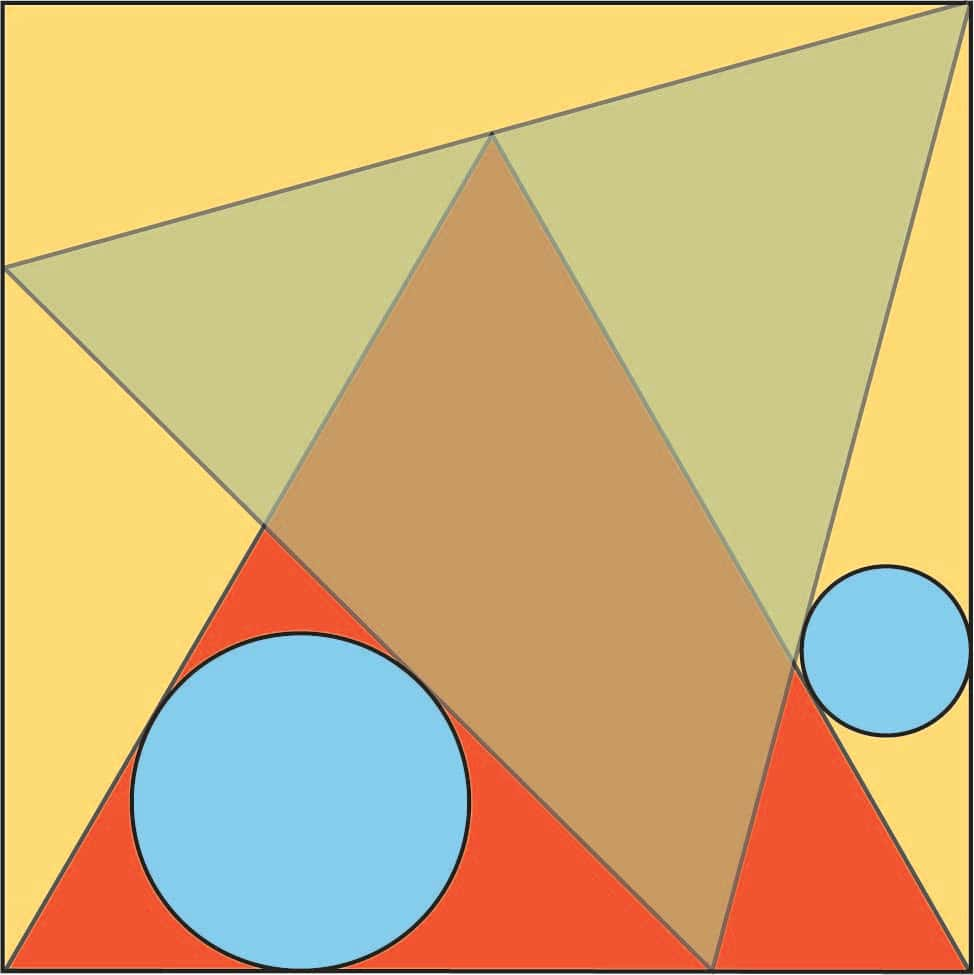
La réponse est 2, le démontrer ne demande que des connaissances de géométrie élémentaire concernant les similitudes et le théorème de Pythagore... mais également de beaucoup d'astuce ! Ici, il est nécessaire d'utiliser de plus un résultat moins connu : le rayon du cercle inscrit dans un triangle est égal à deux fois la surface du triangle divisé par son périmètre. Ainsi, la question passe par le calcul de toutes les longueurs des segments en évidence sur le dessin !
Art et sangakus
En plus de constituer des énigmes mathématiques, les sangakus ont un côté esthétique qui a attiré certains artistes contemporains comme Jean Constant qui, dans l'œuvre suivante s'inspire de la même sangaku :

On trouvera de nombreuses œuvres de Jean Constant sur son site.
Hervé Lehning
En savoir plus sur Hervé Lehning
Normalien et agrégé de mathématiques, Hervé Lehning a enseigné sa discipline une bonne quarantaine d'années. Fou de cryptographie, membre de l'Association des réservistes du chiffre et de la sécurité de l'information, il a en particulier percé les secrets de la boîte à chiffrer d'Henri II.
- Son blog MATH'MONDE sur Futura
- Le dernier livre d'Hervé Lehning :
À découvrir également : L'univers des codes secrets de l'Antiquité à Internet paru en 2012 chez Ixelles.


















