Mathématiques : qu’est-ce qu’une conique ?

Conique est le diminutif de « section conique », c'est-à-dire l'intersection d'un cônecône et d'un plan. Avec cette définition, on voit assez facilement les différentes formes prises par les coniques. De nos jours, on préfère les définir comme courbes du second degré, c'est-à-dire une courbe admettant une équation du second degré, plus pratique pour les calculs mais transformant les coniques en objets abstraits pour beaucoup.

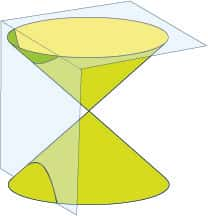
Un cône coupé par un plan

L'intersection du cône de la figure ci-dessus et d'un plan vertical est une hyperbole. Pour un plan horizontal, nous obtenons un cercle. L'effet de perspective le fait ressembler à une ellipse. Entre ces deux cas, quand le plan est parallèle à une génératrice, nous obtenons une parabole. Quand le plan passe par le sommet du cône, on obtient un couple de droites, on parle alors de conique dégénérée.

Photographie d’une pièce d’eau

Quand on photographie un objet, l'image obtenue est la section par le plan de la pellicule (ou du capteurcapteur numériquenumérique) d'un cône dont le sommet est le diaphragmediaphragme de l'appareil et la base est l'objet photographié. Donc, si nous photographions un cercle, nous obtenons toujours une conique. Pour le vérifier, il vous suffit d'aller photographier une pièce d'eau circulaire et de constater que vous obtenez une ellipse.

De façon plus étonnante, elle peut prendre toutes les formes et cela vient tout simplement de la définition des coniques donnée ci-dessus ! Ce sera plus difficile de voir la pièce d'eau comme une hyperbole car, non seulement vous n'en verriez qu'une branche mais il vous faudrait vous placer les pieds dans l'eau !