Comment Marie-Antoinette chiffrait-elle ses lettres ?

Marie-Antoinette chiffrait ses lettres par substitution poly-alphabétique. Pour cela, elle disposait d'une table de chiffrementchiffrement par destinataire. En voici une :

Un des tableaux de chiffrement de Marie-Antoinette. © Archives nationales

On notera que ce tableau ne contient que 22 lettres, les lettres manquantes sont J, K, U et W, ce qui correspond à un usage venant du latin où I et J d'un côté, U et V de l'autre sont confondues. K peut être remplacé par C et W par V.

Clef de chiffrement et utilisation correcte

L'utilisation de cette table pour chiffrer demande une clef secrète qu'on partage avec le destinataire. Par exemple, si la clef est sel, pour chiffrer la première lettre, on utilise la ligne dont la première colonne est ST, D est alors changé en V (et V en D), E en O, etc. Pour chiffrer la seconde, on utilise la ligne dont la première colonne est EF.

Pour chiffrer une phrase comme je vous aime, on peut construire un tableau à 10 lignes et 3 colonnes :

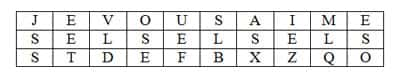
Le message chiffré est donc stdefbxzqo. Si vous essayez de chiffrer une lettre ainsi, vous verrez la difficulté d'éviter les erreurs. C'est pour cela que, on ne sait quel cryptologue avait conseillé à Marie-Antoinette de ne chiffrer qu'une lettre sur deux ce qui, en fournissant des repères, simplifie grandement le chiffrement mais l'affaiblit tout aussi grandement. Nous allons voir pourquoi.

Utilisation par Marie-Antoinette

Le tableau devient ainsi :

 

Le message chiffré est maintenant jovmubasmt. On peut examiner des lettres chiffrées ainsi par Marie-Antoinette aux Archives nationales, comme la suivante :

 
Travail de chiffrement d’une lettre au comte de Fersen où l’on voit que Marie-Antoinette ne chiffrait qu’une lettre sur deux. © Archives nationales

Décryptement

Le décryptement sans connaître la clef est ainsi facilité, surtout si on connaît le tableau de chiffrement. C'est ici que des talents de cruciverbiste sont utiles. En effet, on peut deviner un mot si on en connaît une lettre sur deux comme ici J-V-U-A-M, qui est transparenttransparent pour tout amateur de mots croisés. Ensuite, on sait que la première lettre de la clef transforme E en O ce qui ne se produit que pour ST, en continuant ainsi, on décrypte le message quel que soit sa longueur.