Königsberg, la ville aux 7 ponts qui a donné naissance à la théorie des graphes

Dans la ville de Königsberg aux sept ponts sur le Pregel, un fleuve. Quelle promenade, quelle théorie et quel mathématicienmathématicien ? 

Réponse :

La ville de Königsberg est construite autour de deux îles sur un fleuve. Ces deux îles sont reliées entre elles par un pont et six autres ponts relient les rives du fleuve aux îles comme le montre le plan, ci-dessous : 

© Hervé Lehning, tous droits réservés

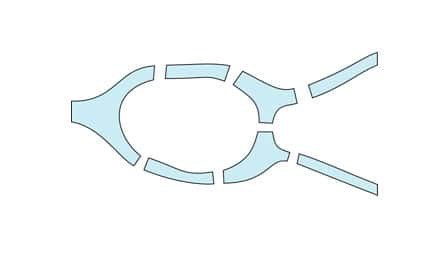
Les habitants se demandaient si l'on pouvait trouver un circuit de promenade, à travers les rues de Königsberg, en partant d'un point au choix et y revenant mais en traversant une et une seule fois chaque pont ?

Léonhard Euler. © DP

Ce désir pouvait sembler étrange mais le mathématicien et physicienphysicien, Leonhard EulerLeonhard Euler (1707 - 1783) résolut la question en initiant la théorie des graphes. Pour cela, il simplifia le plan de Königsberg en un graphe où les nœuds sont les parties de la ville et les arêtes sont les ponts.

Une telle promenade est-elle possible ? © Hervé Lehning, tous droits réservés

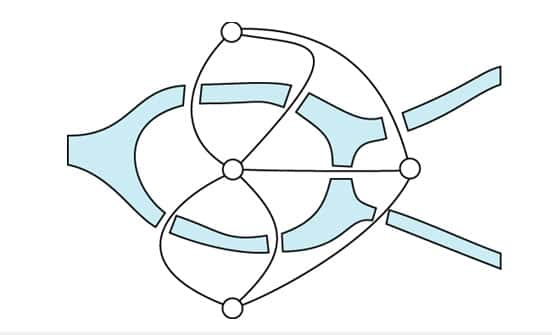
Euler remarqua que, si un trajet existait, de chaque nœud partirait un nombre pair d'arêtes, ce qui n'est pas le cas. La promenade était donc impossible et la théorie des graphes naissait. Depuis, un chemin d'un graphe partant et arrivant au même nœud, en passant une et une seule fois par chaque arête est appelé un cycle eulérien.

À savoir

Au bord de la mer Baltiquemer Baltique, Königsberg est l'ancien nom de l'actuelle ville russe de Kaliningrad. Auparavant, elle fit partie du Royaume de Prusse, puis de l'Empire allemand.