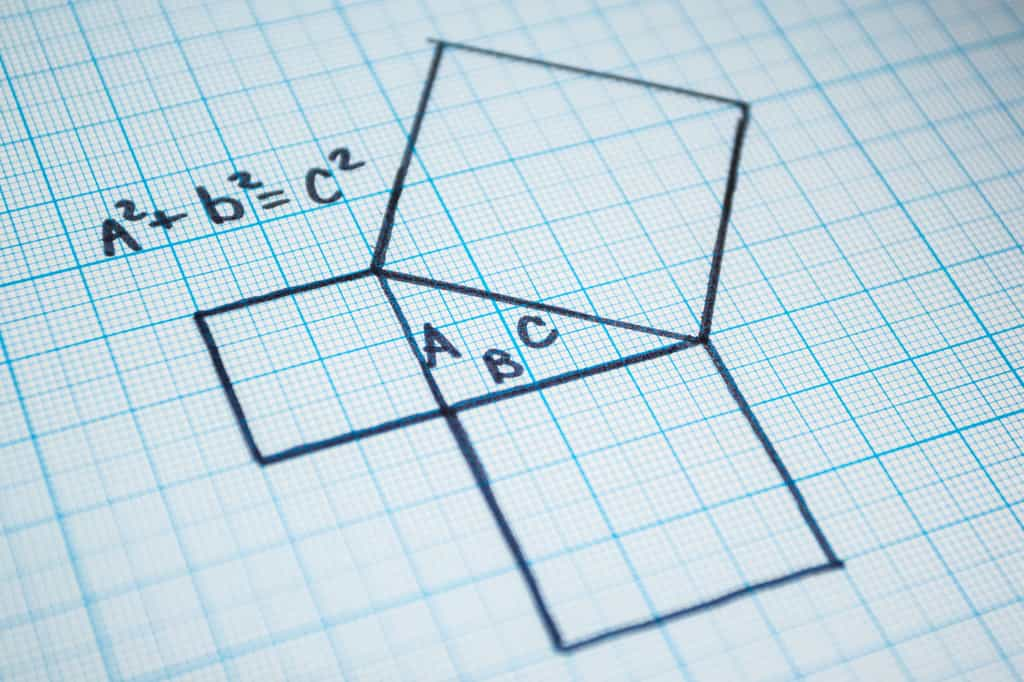
On attribue à Pythagore, le théorème qui affirme que, dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés… et réciproquement : si cette égalité est vraie, le triangle est rectangle.
au sommaire
On retrouve le théorème de Pythagore dans toutes les grandes civilisations. Par exemple, dans la Chine antique, il se nomme le théorème du Gougu et on en trouve une illustration dans le Chou Pei, le plus ancien traité mathématique chinois.
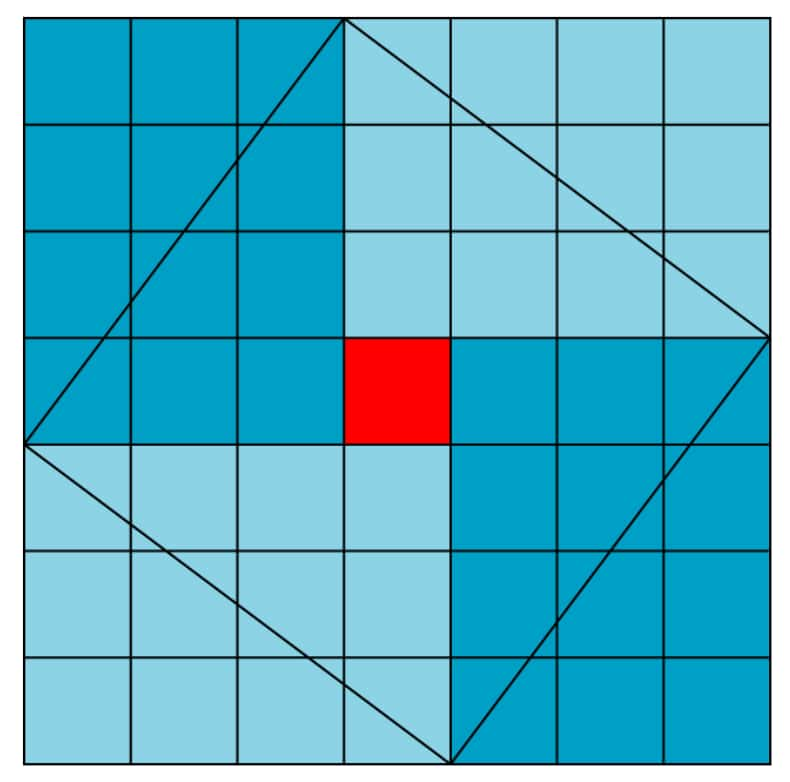
En effet, dans cette figure apparaît un triangle rectangle dont les côtés sont 3, 4 et 5 et une preuve que 32 + 42 = 52''.
Que nomme-t-on triangle égyptien ?
On appelle triangle égyptien, le triangle de côtés 3, 4 et 5. D'après le théorème de Pythagore, ce triangle est rectangle.
Au Moyen Âge, les maîtres d'œuvremaîtres d'œuvre des cathédrales employaient une corde à treize nœuds (de longueur 12 = 5 + 4 + 3) pour tracer les angles droits, utilisant en cela la réciproque du théorème de Pythagore puisque l'égalité 52 = 32 + 42 implique que le triangle de côtés 3, 4 et 5 unités est rectangle.
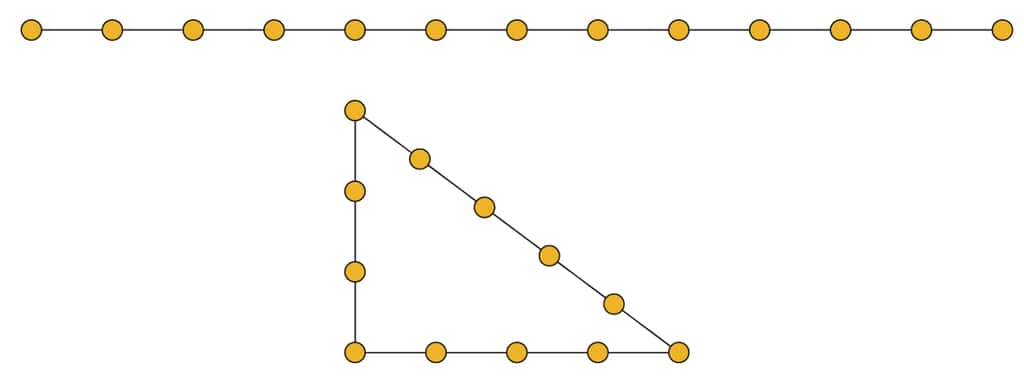
Depuis cette époque, la corde à treize nœuds porteporte le nom de triangle égyptien car les maîtres d’œuvre faisaient remonter son utilisation à l'Égypte antique, ce qui n'est en rien une preuve que cela soit le cas, car aucun texte égyptien n'accrédite cette hypothèse, ce qui ne signifie pas non plus qu'elle soit fausse.
Une signification ésotérique ?
La seule référence antique liantliant ce triplet pythagoricien aux Égyptiens se trouve dans le traité d'Isis et d’Osiris (II, 56) de Plutarque (46 - 125). Les Égyptiens paraissent s'être figuré le monde sous la forme du plus beau des triangles ; de même que Platon, dans sa République, semble l'avoir employé comme symbole de l'union matrimoniale. Ce triangle a son côté vertical composé de 3, la base de 4, l'hypoténuse de 5 parties, et le carré de celle-ci est égal à la somme des carrés des autres côtés. Le côté vertical symbolise le monde, la base la femelle, et l'hypoténuse la progéniture des deux. Le moins qu'on puisse dire est que Plutarque ne voyait pas ce triangle d'un point de vue pragmatique mais plutôt ésotérique, et il en est de même de Platon dans La République (VIII, 546).