Jeu mathématique : le capitaine et la pertuisane

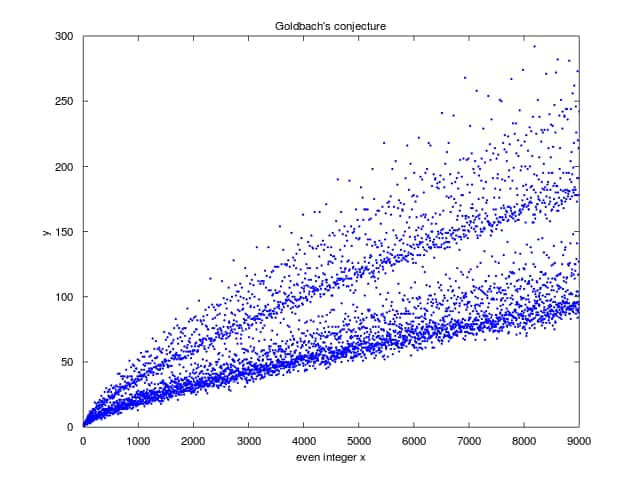
Les nombres premiers sont les nombres divisibles exactement par deux nombres : 1 et eux-mêmes. Ainsi, les plus petits nombres premiers sont 2, 3, 5, 7, 11, 13, etc. Il en existe ainsi une infinité et ils sont à l'origine de questions très difficiles, non résolues à l'heure actuelle et sans doute pour longtemps encore, comme la conjecture de Goldbach, qui date de 1742, selon laquelle tout nombre pair (à partir de 4) serait la somme de deux nombres premiers (par exemple 4 = 2 + 2 ; 6 = 3 + 3 ; 8 = 5 + 3... 20 = 13  + 7 ; etc.) conjecture probablement vraie mais encore jamais prouvée.

La propriété essentielle des nombres premiers est plus simple. La voici : tout nombre entier (non premier) peut s'écrire de façon unique comme produit de nombres premiers.

Ainsi, 10 = 2 x 5 ; 506 = 2 x 11 x 23. Pour effectuer une telle décomposition à la main, on peutftrt essayer de diviser le nombre donné par les nombres premiers dans l'ordre à partir des plus petits : 2, 3, 5, 7, etc. On peut aussi utiliser un logiciellogiciel de calcul formel (il en existe des gratuits). Cela mène à une question mathématico-historique qui peut sembler très éloignée des nombres premiers et rappelle le fameux problème que Gustave Flaubert envoya à sa sœur où il lui demandait l’âge du capitaine sans qu'aucune des données de l'énoncé puisse mener à une solution. Voici une question qui pourrait sembler du même genre :

La comète de Goldbach. © Mucfish, Wikimedia Commons, DP

Question :

Le dernier jour d'un mois de la première guerre mondiale, un obus mit fin aux jours d'un jeune capitaine. Le même jour, dans un pays voisin, un paysan déterrait un pertuisanier, mort dans une grande bataille d'autrefois. Le quantième du mois, multiplié par la longueur en pied de la pertuisane, multiplié par la moitié de l'âge du capitaine, multiplié par le quart du temps (en année) qui séparait ces deux décès est égal à 225.533. On demande l'âge du capitaine.

Réponse :

22 ans. Ce problème à l'énoncé étrange consiste à factoriser 225.533, ce qui est laborieux à la main puisque le plus petit facteur est 7. On trouve d'abord : 225.533 = 7 x 32.219. Le second facteur est 11 : 32.219 = 11 x 2.929. Le diviseur 101 est alors en évidence : 2.929 = 29 x 101 d'où la factorisation :

225.533 = 7 x 11 x 29 x 101

Le dernier jour du mois ne peut donc être que le 29, ce qui implique que l'année est bissextile, donc 1916, seule année bissextileannée bissextile de la Grande Guerre. Il est temps de se renseigner sur ce qu'est une pertuisane. Il s'agit d'une lance utilisée par un soldat à pied aux XV^e et XVI^e siècles. Elle mesure entre 2 et 4 mètres. En évaluant le pied à 30 cm, sa longueur vaut entre 6 et 12 pieds. Vu l'énoncé, elle vaut donc 7 ou 11 pieds. Le quart du temps entre les deux décès ne peut être que 101 et l'âge du capitaine, ne pouvant être 14 ans, est 22 ans et la pertuisane mesure 7 pieds. Le pertuisanier est mort en 1512 donc, probablement à la bataille de Ravenne.