Découvrez les cercles cachés du tore et du Paris-Brest

En mathématiques, les surfaces ayant cette forme sont appelées des tores. Elles sont obtenues en faisant tourner un cercle autour d'un axe de son plan.

© Hervé Lehning, tous droits réservés

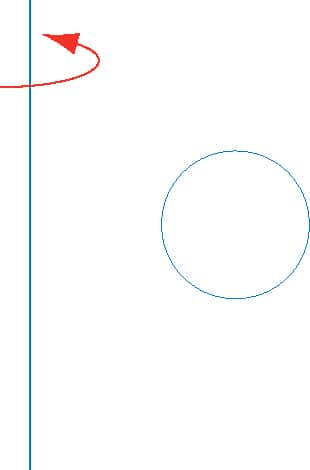
Il s'agit d'une surface de révolution. Les plans contenant l'axe de révolution sont dits plans méridiens, les plans orthogonaux sont dits plans parallèles. Ces définitions sont valables pour toutes les surfaces de révolution, la sphère en particulier. Si le cercle ne coupe pas l'axe, cela donne effectivement une surface en forme de chambre à airair, nommée tore à collier à cause du trou médian.

Une chambre à air. © DP

Par chaque point du tore, il passe donc deux cercles : le cercle méridien et le cercle parallèle, appartenant respectivement au plan méridien et au plan parallèle du point d'où la question. 

Question :

Ces deux familles de cercles sont-elles les seules tracées sur le tore à collier ?

Réponse :

Non, il y en a deux autres : les cercles de Villarceau.

Yvon Villarceau (1813 - 1883) était élève de l'Ecole Centrale de Paris quand il découvrit que l'intersection d'un tore à collier par un plan bitangent était composée de deux cercles, qui portent depuis son nom. Mais qu'est-ce qu'un plan bitangent ? Bien entendu, il s'agit d'un plan tangent en deux points au tore. On les trouve à travers un petit dessin dans un plan méridien.

Intersections des plans bitangents par un plan méridien. © Hervé Lehning, tous droits réservés

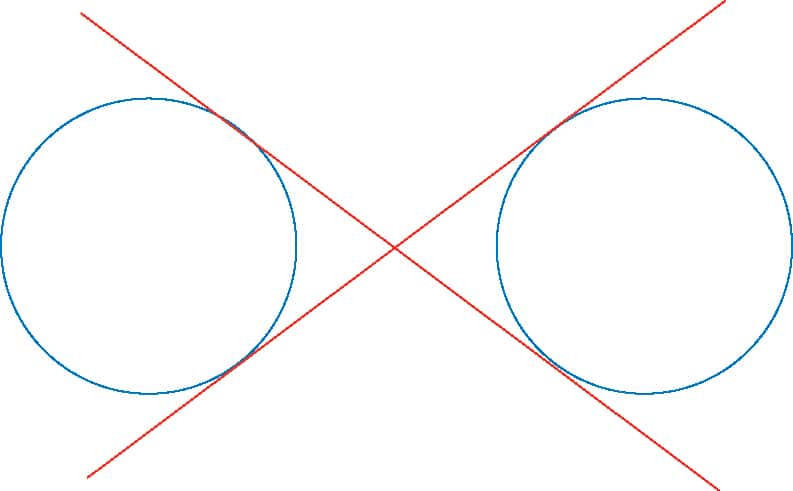
On voit relativement facilement que l'intersection du tore par un plan bitangent est formée de deux ellipses, ce qui était sans doute connu avant Villarceau. L'apport de celui-ci consiste à avoir établi que ces ellipses étaient en fait des cercles.

Cercles de Villarceau vus dans l’espace.

Escalier en vis de Hans Thoman Uhlberger, construit vers 1579. Musée de l'Oeuvre Notre-Dame de Strasbourg © Ji-Elle, wikimedia commons, CC 3.0

Ces formes circulaires dans l’escalier de la cathédrale de Strasbourg, œuvre de Thomas Uhlberger vers 1580 permettent-elles d’affirmer que les cercles de Villarceau était déjà connus à la Renaissance ?