au sommaire
Le chercheur théoricien Philippe BraxPhilippe Brax (interview des pages 3 à 9 de ce dossier) évoque ici ses travaux pour expliquer l'énergie noire et en particulier la théorie des particules caméléons.

On ne peut donc pas faire intervenir une théorie tenseur-scalaire ou f(R) pour expliquer l’énergie noire ?
Philippe Brax : En fait si !
Dans un article, publié en 2004 par Carsten van de Bruck, Anne-Christine Davis, Justin Khoury, Amanda Weltman et moi-même, nous avons montré qu'il existait une théorie tenseur-scalaire [voir la page 6 de ce dossier, NDLRNDLR] dont la masse de la particule associée au champ scalaire était fonction de la densité de l'environnement dans lequel elle se trouvait. Elle serait donc légère dans le vide inter-amas et lourde dans une étoile comme le Soleil.
Cette particule s'adaptant en quelque sorte à son environnement, on lui a tout naturellement donné le nom de « particule caméléon ».
De cette façon, il est possible de concilier aussi bien les observations dans le Système solaireSystème solaire qu'au niveau des amas de galaxiesamas de galaxies.
En fait, ce qui permet de le faire dans le Système solaire, où l'espace interplanétaire est tout de même vide, c'est un effet d'écrantage du champ de caméléons, qui intervient dans une zone formant une coquille à la transition entre, par exemple, la Terre et son environnement immédiat. Ce même mécanisme marche pour le Soleil et il permet d'échapper aux contraintes de Cassini.

La théorie des caméléons peut être décrite dans le cadre de théories f(R). Pourtant, récemment, deux groupes de chercheurs ont annoncé avoir fait des tests de ces théories f(R) avec des observations au niveau des amas de galaxies. Les résultats obtenus, sans vraiment réfuter ces dernières, semblent les rendre assez peu crédibles pour expliquer l’énergie noire. Doit-on en tirer la même conclusion pour la théorie des caméléons ?
Ces tests posent surtout des contraintes sur les différentes théories f(R) possibles, mais certaines conduisent à des prédictions très proches de celles du modèle de concordance ΛCDM. Pour le moment, la théorie des caméléons rentre précisément dans ce cadre et elle reste parfaitement compatible avec les observations. On doit donc améliorer la précision des tests précédents et des missions sont à l'étude pour cela.
Il y a par exemple la mission EuclidEuclid, sur laquelle réfléchit actuellement l'Esa. En mesurant au niveau des galaxies et des amas de galaxies des effets de lentilles gravitationnelleslentilles gravitationnelles faibles, les conséquences des oscillations acoustiques des baryonsbaryons du plasma primordial et l'effet Sachs-Wolfe intégré, elle devrait nous en apprendre plus sur la nature de l'énergie noire. Je fais d'ailleurs partie de l'équipe des théoriciens qui se penche sur le potentiel de la mission Euclid.
On a de bonnes raisons de penser que l’on peut créer de la matière noire dans les collisions de protons au LHC. Est-il possible de produire des particules caméléons en laboratoire et ainsi de tester directement la théorie ?
Remarquablement, il existe deux façons de mettre en évidence l'existence des particules caméléons et il y a même des expériences en cours qui les recherchent. C'est le cas avec l'expérience GammeV qui repose sur l'idée que les caméléons pourraient se comporter de façon assez similaire à l'axionaxion de la chromodynamique quantiquechromodynamique quantique, lorsqu'un rayon laserlaser traverse un champ magnétiquechamp magnétique. Une autre approche fait intervenir des mesures avec la prochaine génération d'expériences sur l'effet Casimireffet Casimir.
En quoi consiste l’expérience GammeV ?
Initialement, c'est une expérience destinée à mettre en évidence l'existence des axions. Ces derniers devraient être produits lorsqu'un rayon laser polarisé pénètre dans une région où règne un champ magnétique important. Il se produit alors un phénomène d'oscillation similaire à ceux des neutrinosneutrinos qui va convertir des photonsphotons en axions. Ceux-ci sont très pénétrants et ne sont donc pas arrêtés par un obstacle opaque ou réfléchissant. Traversant ce dernier et toujours dans un champ magnétique, les axions peuvent se reconvertir en photons. C'est le même principe que pour l'expérience PVLASPVLAS en Italie.
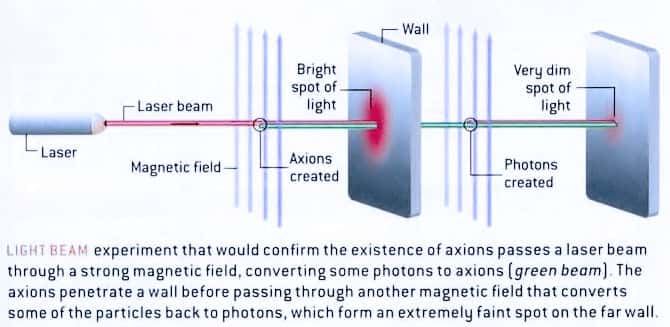
À la différence des axions, lorsque les caméléons s'approchent de l'obstacle et essayent d'y pénétrer, leur masse augmente et ils ne peuvent pas non plus le traverser. Dans l'expérience GammeV, si des caméléons sont produits, on peut donc les accumuler dans une cavité plongée dans un champ magnétique et où pénètre un faisceau laser polarisé. Si l'on coupe le faisceau laser, les caméléons présents vont tout de même finir par se reconvertir lentement en photons tant que règne un champ magnétique intense. On peut donc observer une luminescence rémanente.
Pour le moment, ces expériences n'ont rien donné d'autre que de poser une borne pour la valeur du couplage entre photons et caméléons, c'est-à-dire la probabilité de conversion de ces particules l'une dans l'autre.
Et pour l’effet Casimir, comment peut-on le relier à l’existence de particules caméléons ?
Le champ des particules caméléons peut être vu comme la manifestation d'une cinquième force à très courte portée dans le cadre d'expériences avec l'effet Casimir. En 1948, Hendrik Casimir cherchait à calculer les forces induites par les fluctuations de charges électriques des couches électroniquescouches électroniques entre deux atomesatomes neutres polarisables.
Pour simplifier le problème, il le ramena d'abord à celui d'un seul atome proche d'une plaque métallique conductrice. Cela le conduisit finalement à examiner les fluctuations quantiques du champ électromagnétiquechamp électromagnétique entre deux plaques conductrices. Il découvrit que les deux plaques modifiaient la forme des fluctuations quantiques du vide dans l'espace qu'elles encadrent, y changeant sa densité d'énergie qui devient localement plus faible.
Une densité d'énergie peut se voir comme une pressionpression, ce qui fait que la pression de l'énergie dans le vide environnant, plus forte, va pousser les plaques l'une vers l'autre. Cet effet a depuis été vérifié en laboratoire de nombreuses fois.
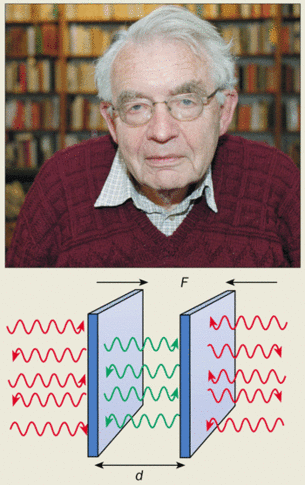
Avec des collègues, C. van de Bruck, A. C. Davis, D. J. Shaw et D. Iannuzzi, nous avons calculé que, dans certaines expériences avec l'effet Casimir, en considérant des plaques séparées par quelques dizaines de micromètresmicromètres, la force attractive entre les deux plaques induites par les particules caméléons entrait en compétition avec celle de l'effet Casimir.
Le phénomène n'est pas facile à mettre en évidence mais une prochaine génération d'expériences pourrait tester la théorie des particules caméléons de cette façon, en montrant une déviation bien spécifique par rapport aux prédictions basées sur la seule prise en compte de l'effet Casimir.