Supraconductivité : explications du phénomène

Pour expliquer le phénomène de la supraconductivité, commençons par une petite introduction de physique quantique ! Le mot clé est : quantum ! Un quantum d'énergie qui correspond à une quantité d'énergie de la dualité onde - corpusculecorpuscule ! L'énergie ne peut s'échanger que par quanta : la discontinuité est de mise en physique !

Oscillateur à cristal ( 25 MHz ). © Slick - Domaine public 

Les phonons sont au son, ce que les photons sont à la lumièrelumière! Par définition, le photon est la plus petite unité d'énergie que peut posséder un mode de vibrationvibration lumineuse, tandis que le phonon est la plus petite quantité d'énergie que peut posséder un mode de vibration cristalline (vibration des atomesatomes dans un solidesolide).

Dans un cristal (un type de solide), les atomes sont placés de manière très ordonnée. Ce sont les forces interatomiques qui leur confèrent leur arrangement spécifique. Ces forces jouent le même rôle que les ressorts dans un système « massesmasses-ressorts ». Par conséquent, si on déplace légèrement un atome de sa position initiale et qu'on le relâche, il se mettra à osciller, comme un pendule. Étant donné que cet atome est relié aux autres par les forces électrostatiquesélectrostatiques qui agissent entre eux, les autres atomes du cristal se mettront eux aussi à vibrer, d'où le nom vibration cristalline ! Il y aura alors propagation d'une onde de déformation dans le solide.

Les atomes d'un cristal forment une structure vibrante. Un courant qui circule correspond à un déplacement d'électronsélectrons. Leur propagation s'accompagne de chocs : ils rebondissent sur différents obstacles (impuretés, défauts de structure...) et ces rebonds non élastiques s'accompagnent d'une perte d'énergie sous forme de chaleurchaleur : c'est le célèbre effet Jouleeffet Joule !

Théorie BCS

Cette théorie est basée sur le couplage des électrons d'un métalmétal en paire : les paires de Cooper. Elles forment un état unique, cohérent, d'énergie plus basse que celui du métal normal (électrons non appariés).

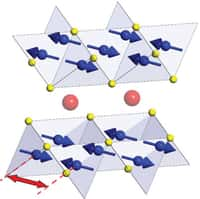
Le problème est d'expliquer cet appariement compte tenu de la répulsion coulombienne. Dans un métal, les électrons interagissent avec le réseau cristallinréseau cristallin formé d'ionsions positifs. Ceux-ci attirent les électrons et se déplacent légèrement (grande inertieinertie). Les physiciensphysiciens ont donné le nom de phonons à ces vibrations atomiques naturelles. Cette interaction entre les électrons et les phonons est à l'origine de la résistivitérésistivité et de la supraconductivité : attirés par le passage très rapide d'un électron (10+6 m/s), les ions se déplacent et créent une zone locale électriquement positive. Compte tenu de l'inertie, cette zone persiste alors que l'électron est passé, et peut attirer un autre électron qui se trouve ainsi, par l'intermédiaire d'un phonon, apparié au précédent. Et ce malgré la répulsion coulombienne. L'agitation thermique finit par détruire ce fragile équilibre d'où l'effet néfaste de la température.

La théorie BCS. © DR

La théorie quantique nous enseigne que les électrons dont le spinspin vaut + ou - 1/2, obéissent au principe d'exclusion de Pauliprincipe d'exclusion de Pauli ; ainsi deux électrons de même spin ne peuvent occuper le même état d'énergie et il s'ensuit qu'il ne peut cohabiter que deux électrons par état d'énergie. Les états de basse énergie vont donc vite se saturer et l'énergie totale du système sera plus importante que si tous les électrons étaient dans le même état de plus basse énergie. La paire de Cooper permet un état d'énergie global plus faible donc plus stable. En effet, celle-ci se comporte comme un bosonboson, c'est-à-dire une particule de spin entier, par opposition aux fermionsfermions de spin demi-entier comme les électrons.

Cela est important car seules les particules de spin demi-entier sont soumises au principe d'exclusion de Pauli. La paire de Cooper en tant que boson est soumise à la condensation de Bose-Einsteincondensation de Bose-Einstein, un état particulier de la matièrematière à basse température caractérisé par la possibilité pour les bosons d'occuper en nombre illimité le même état d'énergie, le plus bas. On appelle la différence d'énergie entre le matériaumatériau supraconducteursupraconducteur contenant des paires de Cooper et le matériau à l'état normal, le GapGap.

Comme l'agitation thermique augmente, les paires de Cooper disparaissent et le Gap diminue jusqu'à valoir zéro. On est alors à la température critiquetempérature critique et le matériau passe dans son état normal. Les paires de Cooper, on l'a vu, sont soumises à la condensation de Bose-Einstein. Cet état particulier a une autre propriété des plus intéressante : les bosons soumis à cette condensation peuvent traverser un réseau sans rencontrer d'obstacles. Les paires de Cooper peuvent ainsi circuler sans rencontrer la moindre résistancerésistance, d'où la supraconductivité.