au sommaire

Voyage dans le temps : l'article de Morris-Thorne-Yurtsever
En 1988, Thorne, Morris, et Yurtsever révélèrent le résultat de leurs calculs avec l'énergie négative ainsi que leur incroyable implication dans l'article intitulé Wormholes, Time Machines, and the Weak Energy Condition.

Non seulement il était théoriquement possible d'ouvrir un passage entre deux points de l'espace et de le traverser sans encombre pour voyager entre les étoiles de façon quasi instantanée, mais on devait aussi pouvoir voyager dans le temps !
Regardons cela d'un peu plus près
La métrique solution des équations d'EinsteinEinstein qu'ils trouvèrent est la suivante :
Elle ressemble à celle de Schwarzschild pour l'intérieur d'une étoile et elle doit satisfaire des conditions de décroissance à l'infini pour se raccorder à un espace-temps plat de Minkowski.
Voilà comment cela marche, et c'est tout simple
Ayant ouvert un trou de ver traversable, et en supposant celui-ci très stable, on peut imaginer laisser une de ses bouches d'entrée sur Terre alors que la seconde pourra être emportée à l'intérieur d'un vaisseau spatial en vol relativiste effectuant un aller-retour de (disons) 1.000 ans pour un observateur resté sur Terre.
Si la vitesse pendant le trajet est très proche de la lumièrelumière, il pourra ne s'être écoulé que quelques heures ou quelques jours dans le vaisseau. On est précisément dans le cas célèbre des jumeaux de Langevin.
Il existera donc alors un décalage temporel entre les deux bouches du trou permettant de remonter dans le passé jusqu'à 1.000 ans avant le retour du vaisseau sur Terre ou dans le futur jusqu'à 1.000 ans après le départ du vaisseau pour quelqu'un resté sur la Planète.
C'est ce qu'on voit sur le diagramme d'espace-tempsdiagramme d'espace-temps ci-dessous repris des cours de Thorne à Caltech (Methusalem restant sur Terre alors que Florence effectue son voyage interstellaire).
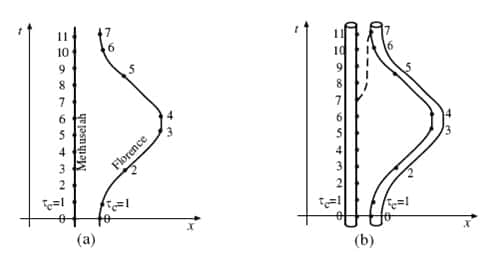
Il y a quand même un « petit » problème. Matt Visser, un physicienphysicien spécialisé dans la théorie des trous de ver, a fait les estimations suivantes.
Si l'on devait construire un trou de ver stable de 1 m de diamètre, il suffirait de « tapisser » la bouche du trou de ver de seulement 10-21 m d'énergie négative, soit moins d'un millionième de la taille d'un protonproton. Là où cela coince c'est qu'il faudrait disposer de l'énergie libérée par 10 milliards d'étoiles en une année !

La conjoncture de la protection chronologique de Hawking
En 1992, Hawking a fait toute une série de calculs pour essayer de prouver que l'on ne peut pas modifier le passé car aucune boucle du genre temps ne pourrait exister autrement que pour les particules élémentairesparticules élémentaires. Sans en donner une démonstration complète, les résultats qu'il a obtenus sont nettement défavorables.
Sa conclusion finale est célèbre : « La meilleure preuve que les voyages dans le temps sont impossibles est que nous ne sommes pas envahis par des hordes de touristes venues du futur ».
On peut mettre en relation ses raisonnements avec le phénomène suivant.
Un effet Larsen ?
Le plus grave problème que pose la possibilité de créer un trou de ver traversable est celui lié à un effet bien connu que l'on appelle l'effet Larsen (du nom du physicien danois Søren Larsen (1871-1957). Nous avons tous un jour ou l'autre été confrontés au problème d'un coup de téléphone amplifié de façon stridente par un haut-parleur. Le téléphone enregistre le son émis par le haut-parleur qui est alors renvoyé au correspondant pour être enregistré à son tour et réémis à l'aide du haut-parleur, etc.
De manière similaire, des ondes électromagnétiquesondes électromagnétiques (par exemple) voyageant vers le passé dans le trou de ver pourraient à nouveau l'emprunter dans le futur et ainsi de suite. De l'énergie positive s'accumulera donc dans le trou de ver ce qui finira par contrebalancer l'énergie négative responsable du caractère traversable du trou de ver.
La question centrale est « Ok mais en combien de temps ? ».
Les calculs faits jusqu'à présent montrent que c'est si rapide qu'un objet « macroscopique » n'aurait pas le temps de traverser la bouche du trou avant qu'il ne se ferme. Cependant la réponse ultime est enfouie dans les lois de la gravitation quantiquegravitation quantique non perturbative, une théorie encore à naître.
Des voyages supraluminiques seraient donc peut-être encore possibles dans l'espace, mais dès qu'on essaierait de voyager dans le temps les lois de l'universunivers conspireraient pour l'empêcher. C'est aussi la conclusion à laquelle est arrivé Igor Novikov, l'ancien collaborateur principal du grand Zeldovich.
Le principe d'autocohérence de Novikov

Le problème du grand-père est une objection classique au voyage dans le temps. Si vous remontez dans le temps pour tuer votre grand-père alors vous n'existez pas donc vous ne remontez pas dans le temps et votre grand-père est toujours vivant donc vous allez le tuer, etc.
Ne pourrait-on pas cependant considérer des types de voyage dans le temps possibles ? C'est ce que Novikov et d'autres ont voulu savoir. Les résultats que donnent les équations de la relativité généralerelativité générale (RG) sont illustrés par l'exemple suivant.
On pourrait imaginer une bille lancée vers la bouche d'un wormhole et émergeant dans son propre passé pour se percuter et s'empêcher de rentrer dans la bouche de celui-ci. C'est une version physiquement simple à traiter du paradoxe du grand-pèreparadoxe du grand-père. Inversement on pourrait avoir une boule se percutant pour se forcer à aller dans le wormhole. Tout calcul fait, seule cette dernière solution est autorisée par la RG classique semble-t-il.
Pour arriver à cette conclusion, Novikov et ses collaborateurs se sont appuyés sur des calculs relativement élémentaires mais reposant sur un des principes les plus fondamentaux de la physiquephysique, celui de moindre action.