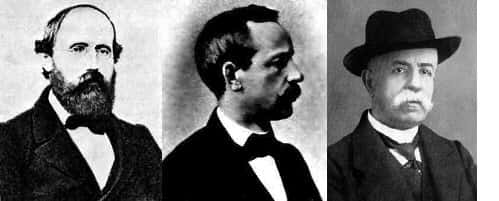au sommaire

L'espace-temps de Minkowski
Il existe de profondes relations entre les concepts de la relativité restreinte et ceux de la théorie électromagnétique de Maxwell-Lorentz. Historiquement l'une a d'ailleurs été à l'origine de l'autre. On définit un champ électrique comme la donnée de l'intensité de ce champ en tout point de l'espace. Pourquoi ?
Donnons-nous une petite boule chargée au bout d'un ressort en un point de l'espace. Si le ressort s'étire (ou se compresse) on dira qu'une force électrique était présente. Par extension si l'on pouvait imaginer une série d'appareils du même genre partout dans l'espace, on aurait une infinité de valeurs de forces pouvant s'exercer sur des charges test au bout de ressorts.
Si les forces changent dans le temps on pourra donc décrire la dynamique de l'ensemble de celles-ci par la dynamique d'un champ de forces, le champ étant cette distribution de force en tout point de l'espace.
La théorie électromagnétique est donc, par certains côtés, la théorie mécanique déguisée d'un ensemble infini et continu de points élémentaires chargés représentant l'état du champ électromagnétique en tout point de l'espace.
Le concept d'espace-temps
Ce qu'EinsteinEinstein a vu est que cette mécanique déguisée, liée à la possibilité de propagation d'une onde lumineuse, était en contradiction avec la mécanique usuelle de Newton.
Afin de résoudre cette contradiction, il fut amené à remettre en question les concepts de temps et d'espace de la physique classique. Pour cela on doit considérer une infinité d'observateurs en chaque point de l'espace et possédant, au lieu de l'appareil décrit précédemment, une règle et une horloge et effectuant des mesures de temps et d'espace pour chaque événement physique.
L'ensemble de ces événements, comme une explosion ou l'arrivée d'un train en gare, auxquels on coordonne des valeurs de temps et d'espace est justement ce qu'on appelle l'espace-tempsespace-temps.
De cette manière, et en modifiant la validité universelle de l'écoulement du temps et des valeurs spatiales attribuées aux événements, on peut résoudre les contradictions entre la mécanique de Newtonmécanique de Newton et l'électromagnétismeélectromagnétisme de Maxwell. C'était par exemple le cas avec l'invariance de la vitesse de la lumièrevitesse de la lumière pour tous les observateurs, mise en évidence par l'expérience de Michelson-Morley.
Cette invariance est à la source des fameuses transformations de Lorentz, lesquelles découlent directement de l'exigence suivante : une sphère de lumière doit en rester une en passant d'un référentielréférentiel en mouvementmouvement rectiligne uniforme à un autre.
La géométrie de l'espace-temps
La théorie ainsi obtenue conduisit Minkowski à introduire une géométrie nouvelle pour les événements du monde, la géométrie de l'espace-temps. Tous les effets de la relativité restreinte d'Einstein peuvent être vus comme dérivant de cette géométrie.
En effet ces transformations forment ce qu'on appelle un groupe et l'on sait depuis Félix Klein qu'à un groupe de transformations données doit correspondre une géométrie donnée. Selon le fameux programme d'Erlangen de Klein on peut donc étudier en profondeur une géométrie si l'on connaît son groupe fondamental de transformations. Inversement, si l'on connaît des équationséquations invariantes selon un groupe donné, on peut traduire géométriquement de façon déterminée le contenu de celles-ci.
La théorie générale liantliant groupes et géométries vers la fin du XIXe siècle est ce qu'on appelle la théorie des invariantsinvariants. Il était donc naturel pour Minkowski d'utiliser systématiquement son espace pour discuter des conséquences des découvertes d'Einstein sur l'ensemble des lois régissant les phénomènes dans l'espace et le temps. On ne surprendra pas le lecteur un peu initié en faisant remarquer que la théorie des invariants utilise de façon centrale la notion de tenseurstenseurs, dont les vecteurs sont des cas particuliers. Bien qu'introduite par Minkowski lui-même, on en parlera peu ici.
Il est cependant important de bien voir, déjà, qu'on peut faire intervenir des quadrivecteurs dans cette géométrie quadridimensionnelle qui sont la généralisation naturelle des trivecteurs de l'espace.

Hermann Minkowski et Félix Klein ont théorisé certaines questions autour du concept d'espace-temps. © DR
Le diagramme d'espace-temps
Un moyen très puissant de faire de la relativité est ainsi d'introduire le concept de diagramme d'espace-tempsdiagramme d'espace-temps.
Liés à cela sont les trois concepts fondamentaux suivants :
- 1°) La métrique
Celle-ci définit la valeur du carré de la norme du quadrivecteur entre deux points de l'espace-temps. On parle d'intervalle entre deux événements en chacun de ces points et il s'exprime dans un référentiel donné par :
En utilisant la « matrice » ci-dessous, correspondant justement à la métrique de l'espace-temps,
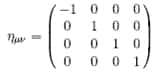
on peut réécrire l'intervalle précédent sous la forme :
Depuis Einstein, on adopte la convention suivante pour de telles expressions. La présence d'indices répétés en haut et en bas indique en fait une sommation sur l'indice avec toutes les valeurs,0,1,2,3 pour t,x,y,z.
On parle aussi de tenseur métrique pour
En changeant de référentiel, pour passer dans celui en translationtranslation rectiligne uniforme à la vitesse v par rapport au second, on donne de nouvelles valeurs aux coordonnées des événements précédents. Toutefois l'intervalle déterminé par la métrique ne change pas, c'est précisément un invariant sous les transformations de Lorentz.
Il s'exprime sous la forme :
où
avec
sont les expressions de ces fameuses transformations (on a posé c=1).
- 2°) Le cône de lumière
Si l'on veut représenter un flashflash de lumière émis en un point de l'espace-temps, et correspondant à une sphère de lumière en expansion, il est commode de supprimer une dimension d'espace. On peut alors le représenter par un cônecône comme dans le diagramme d'espace-temps ci-dessous.
Au fur et à mesure que le temps passe, la sphère de lumière grandit et cela correspondra bien à l'augmentation de la taille d'une section de ce cône.
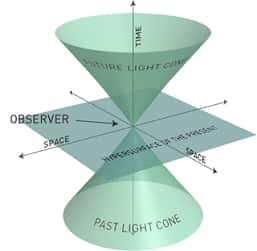
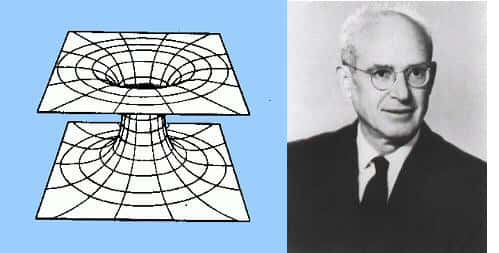
Le cône de lumière, vu selon un observateur (observer) en un point de l'espace. Au fil du temps qui passe, la sphère de lumière grandit. Les deux cônes représentent le passé (past light cone) et le futur (future light cone) sur l'ordonnée du temps (Time). © DR
Comme dit précédemment, on peut introduire un calcul avec des vecteurs généralisant celui dans l'espace de la physique prérelativiste. On parlera alors de quadrivecteurs, le plus simple exemple étant bien sûr celui reliant deux événements dans l'espace-temps et donc deux points dans l'espace de Minkowski.
Si l'on prend le carré de la norme d'un tel vecteur, on retombe sur l'intervalle d'espace-temps. Prenons comme origine la position de l'observateur du schéma ci-dessus.
Selon que l'autre point est à l'intérieur ou non du cône de lumière, on aura les distinctions suivantes :
- à l'intérieur l'intervalle est négatif, il est dit de genre temps et correspond à la possibilité pour l'observateur d'influencer d'une façon ou d'une autre ce qui se passera dans le futur en ce point ;
- sur le cône de lumière, l'intervalle est dit nul et correspond à la possibilité d'influencer le futur pour l'observateur en envoyant un signal à la vitesse de la lumière vers le point considéré ;
- hors du cône de lumière, l'intervalle est alors positif et est dit du genre espace. Il ne peut y avoir aucune relation de cause à effet entre l'observateur et le point considéré car cela impliquerait de dépasser la vitesse de la lumière lors de l'envoi d'un signal.
De manière générale, tous les quadrivecteurs ont un carré de norme possédant une valeur tombant dans les trois classes décrites précédemment. Ils seront respectivement dit de genre temps, nul (ou lumière), espace.
Enfin les deux cônes définissent respectivement les régions passées et futures pouvant être en relations causales avec l'observateur.
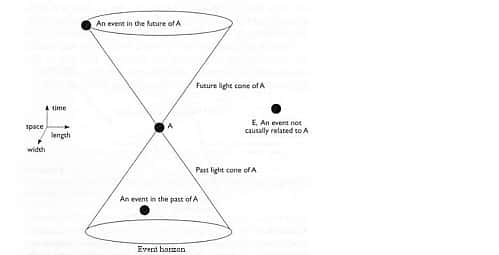
Les deux cônes définissent respectivement les régions passées et futures pouvant être en relations causales avec l'observateur. © DR
- 3°) La structure causale
C'est un concept de la plus haute importance pour toute la suite du dossier, on peut même dire qu'il précède la notion de métrique lorsque l'on veut construire la géométrie des événements spatiotemporels. On introduit pour cela un véritable champ de cônes de lumière en chaque point de l'espace-temps de Minkowski.
Au passage, on rappelle qu'en physique un champ est l'association d'une quantité mathématique, comme un nombre ou un vecteur, en chaque point de l'espace. Des exemples bien connus sont la température, la pressionpression ou la vitesse du ventvent. Dans le cas présent la métrique permet de construire en chaque point de l'espace-temps un cône.

Quand l'espace-temps est plat et statique, les cônes sont tous « rigidement » fixés. Extrait de Cern yellow report 91-06. © Ruth M. Williams
On peut ensuite introduire les horloges, les règles et des ensembles de courbes dans l'espace-temps, c'est-à-dire les trajectoires spatiotemporelles des objets dans celui-ci. On parle de congruences pour un tel ensemble de courbes lorsque celles-ci sont plus ou moins parallèles, retenez bien ce terme.
La lumière étant une horloge (pulsation) et une règle naturelle (longueur d'ondelongueur d'onde) dont les propriétés sont faciles à mesurer précisément, des trajectoires de rayons lumineux seront très importantes pour exhiber les particularités de l'espace-temps. Elles joueront un rôle similaire aux lignes de courant en hydrodynamique pour interpréter les phénomènes de la mécanique des fluides.
On parlera de congruence de courbes aussi bien pour les lignes de courant que pour des trajectoires de photonsphotons dans l'espace-temps. La structure des événements dans l'espace-temps, ainsi que sa dynamique - car comme nous l'apprend la relativité généralerelativité générale, celui-ci est courbe et susceptible de changement - est traduite par la donnée de ces règles-horloges et d'un véritable champ de cône en chaque point de l'espace-temps.
Quand l'espace-temps est plat et statique, les cônes sont tous « rigidement » fixés (cf le schéma ci-dessus). Ce ne sera plus le cas lorsque l'espace-temps sera courbe et dépendant du temps.
Résumé de la théorie de l'espace-temps de Minkowski
En résumé la théorie de l'espace-temps de Minkowski repose sur :
- la notion d'événement ;
- des règles et des horloges ;
- des cônes de lumières ;
- l'intervalle d'espace-temps défini par une métrique ;
- des lignes d'universunivers avec des congruences de courbes.
La conséquence la plus spectaculaire de cette géométrie de l'espace-temps est la dilatationdilatation du temps illustrée par le paradoxe des jumeaux de Langevin.
C'est l'exemple bien connu de deux jumeaux dont l'un reste sur Terre alors que l'autre effectue un voyage aller-retour à une vitesse proche de la lumière entre la Terre et un point distant de 20 années-lumièreannées-lumière par exemple.
À son retour, presque 40 années se seront écoulées sur Terre alors que lui pourra n'avoir vieilli que de quelques jours seulement.
Ceci n'est pas de la science-fiction ! Des horloges atomiqueshorloges atomiques ultraprécises ont été utilisées lors de voyages en avion ou en fuséefusée autour du globe et on a invariablement vérifié non seulement ce phénomène mais aussi les prédictions exactes des équations de la relativité d'Einstein. Sans parler de la désintégration des muonsmuons dans les rayons cosmiquesrayons cosmiques ou en accélérateurs qui vivent d'autant plus longtemps pour un observateur fixe sur Terre qu'ils se déplacent rapidement par rapport à lui. Encore une fois l'accord avec les prédictions des équations de la relativité est remarquable.
Cette dilatation du temps est capitale pour qui veut comprendre comment un trou de ver peut être utilisé pour voyager dans le temps comme il a été proposé à la fin des années 1980 par Kip Thorne.