au sommaire
Résultats récents : l'exemple du LEP
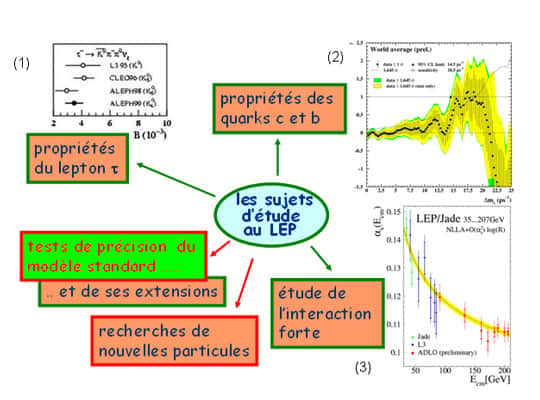
Les sujets étudiés au LEP sont très variés, comme l'illustre schématiquement la Fig. 14.

Fig. 14 : panorama des sujets étudiés au LEP. Les 3 résultats présentés sont : 1) les mesures de l'un des taux de désintégration du tau, par ALEPH et L3 (comparées à la mesure faite par une expérience américaine) ; 2) la mesure, moyennée sur les quatre expériences, de l'amplitude «d'oscillation» du B0s, particule issue des quarks b et s, qui a la caractéristique de se transformer en son anti-particule au cours du temps ; 3) la mesure, moyennée sur les quatre expériences, de la variation de l'intensité de l'interaction forte avec l'énergie à laquelle cette intensité est mesurée.
Dans cette section, on abordera les deux sujets les plus importants, à savoir les tests de précision du modèle standard et la recherche du boson de Higgs standard. Les tests de précision s'appuient sur les mesures de la masse des bosons W (effectuées au LEP et au Tevatron) et de celle du quark top (effectuée au Tevatron), et sur les mesures de nombreuses propriétés du boson Z (faites surtout au LEP, mais aussi au SLC, collisionneur électronélectron positronpositron linéaire de 91 GeVGeV d'énergieénergie situé aux Etats-Unis et ayant fonctionné à plus basse statistique que le LEP durant la même période). On prendra comme seul exemple la mesure de la masse du Z au LEP. La Fig. 15 représente la courbe de résonancerésonance du Z mesurée par ALEPH au cours de la phase LEP 1.
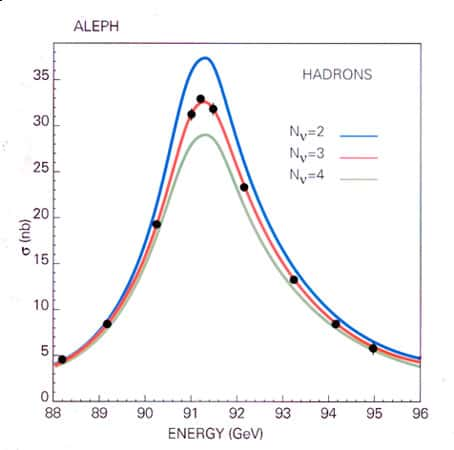
Fig. 15 : courbe de résonance du Z dans le mode quark anti-quark mesurée par ALEPH et comparée à trois prédictions théoriques correspondant à un nombre d'espèces de neutrinos légers de 2, 3, comme dans le modèle standard, ou 4.
Les points expérimentaux sont comparés aux courbes théoriques obtenues pour trois hypothèses sur le nombre d'espècesespèces de neutrinosneutrinos légers (c'est-à-dire de masse inférieure à la moitié de la masse du Z), à savoir 2, 3 ou 4. Toute espèce de neutrino léger ouvre un canal de désintégration pour le Z, donc modifie son temps de vie et, partant, la largeur et la hauteur de la courbe de résonance, ce qui explique les différences notables entre les courbes de résonance obtenues pour 2, 3 ou 4 espèces de neutrinos. La précision expérimentale des points de mesure permet sans ambiguïté de rejeter les hypothèses de 2 et 4 neutrinos légers. Plus quantitativement, en combinant les résultats des quatre expériences afin d'accroître la statistique, on obtient la valeur suivante pour le nombre de neutrinos légers:
Nν = 2,9840 ± 0,0082
Il n'y a donc que trois familles de constituants élémentaires sur le modèle de celles que nous connaissons déjà (c'est-à-dire avec un neutrino léger et fortement couplé au Z). Rappelons qu'avant le LEP, la seule autre indication sur le nombre de familles avec neutrinos légers venait de la cosmologiecosmologie et s'établissait à 4 familles au plus. De la courbe de résonance on déduit également la valeur de la masse du Z. En combinant les résultats des quatre expériences, il vient :
MZ = 91,1875 ± 0,0021 GeV
La précision atteinte sur MZ est de 2.10-5, à comparer à 1% avant le LEP. Cette précision met MZ au rang des constantes fondamentales de la physique des particules élémentairesphysique des particules élémentaires.
Mais la précision de mesure n'est pas une fin en soi. En fait, elle était indispensable au LEP car le but poursuivi était de mesurer des effets quantiques extrêmement fins, appelés « corrections quantiques ». Des exemples en sont donnés sur la Fig. 17 qui illustre le premier ordre des corrections quantiques au processus décrit sur la Fig. 16 à l'ordre le plus bas du développement en perturbations de la théorie.
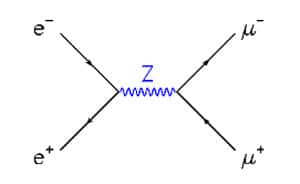
Fig. 16 : annihilation d'une paire électron positron en paire muon anti-muon, par le chemin le plus probable en théorie quantique (i.e. donné par l'ordre le plus bas du développement en perturbations de la théorie) : l'état intermédiaire est un Z.
Considérons le diagramme de la Fig. 17. a) : alors que le quark top a une masse trop élevée pour qu'un Z se désintègre en paire top anti-top qu'on pourrait détecter dans les appareillages, les corrections quantiques permettent la matérialisationmatérialisation pendant un temps très bref de paires top anti-top «virtuelles» au sens de paires dont les éléments ont les mêmes nombres quantiquesnombres quantiques qu'un quark top mais une masse bien plus faible, respectant la loi de conservation de l'impulsion et de l'énergie. Mais, fait extraordinaire, ces corrections dépendent de la masse véritable du quark top, Mtop, et on peut montrer que cette dépendance va comme le carré de Mtop. De même, les corrections quantiques permettent la matérialisation d'un boson de Higgs virtuel lors de la propagation du boson Z intermédiaire (Fig. 17.b) ; dans ce cas, les corrections quantiques vont comme le logarithme de la masse véritable du boson de Higgs, MH. Tout l'intérêt d'une mesure précise des corrections quantiques réside dans la possibilité de contraindre par l'expérience les paramètres clefs du modèle standard, tels que les masses du quark top et du boson de Higgs, sans les mesurer directement.
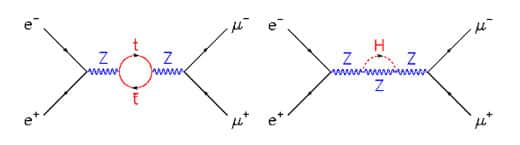
Fig. 17 : annihilation d'une paire électron positron en paire muon anti-muon, par des chemins moins probables de la théorie quantique (tels que donnés par l'ordre 1 du développement en perturbations de la théorie) : on trouve
a) un Z qui se matérialise pendant un temps très bref en une paire top anti-top virtuelle,
b) un Z qui émet puis réabsorbe un boson de Higgs H virtuel.
Une fois atteinte la précision expérimentale requise, les tests du modèle standard consistent à comparer, sur un même ensemble d'observables, les mesures expérimentales et les prédictions théoriques qui sont fonction de Mtop et MH pour en déduire les valeurs les plus probables de ces paramètres, c'est-à-dire les valeurs de ces paramètres qui conduisent au meilleur accord entre données et prédictions. La précision expérimentale des mesures se reflètera directement dans l'incertitude sur le résultat de telles dérivations. Ainsi, en combinant toutes les mesures de précision, sauf évidemment la mesure directe de Mtop au Tevatron, la valeur de la masse du top a pu être prédite :
Mtop = 179,4-9 +12 GeV
Cette prédiction est en très bon accord avec la mesure directe de Mtop au Tevatron, qui seul a l'énergie nécessaire pour produire des quarks top dans les états finals de collision :
Mtop = 172,7 ± 2,9 GeV
La Fig. 18 illustre également cette comparaison. Le très bon accord entre théorie et expérience valide le modèle standard jusque dans sa description des effets quantiques les plus fins de l'interaction électrofaible. Pour mesurer la portée de la prédiction de la valeur de Mtop, on peut rappeler comment on a progressé dans la recherche du quark top. Avant le démarrage du LEP, le bilan des recherches infructueuses permettait d'établir que la masse du top était supérieure à 60 GeV. En 1993, les premières mesures de précision au LEP donnaient comme prédiction 166 GeV avec une marge de +25 GeV et -29 GeV. Enfin, en 1995, le Tevatron observait le quark top et effectuait une première mesure de sa masse à 180 GeV à 12 GeV près, en accord avec la prédiction établie à partir des mesures de précision. Depuis, prédiction indirecte et mesure directe ont gagné en précision par suite principalement de la statistique supplémentaire accumulée.
De même que pour la masse du top, les mesures de précision permettent de contraindre la masse du boson de Higgs, MH. Cet ajustement est cependant moins précis que celui de Mtop, car les corrections quantiques ne dépendent que du logarithme de MH.
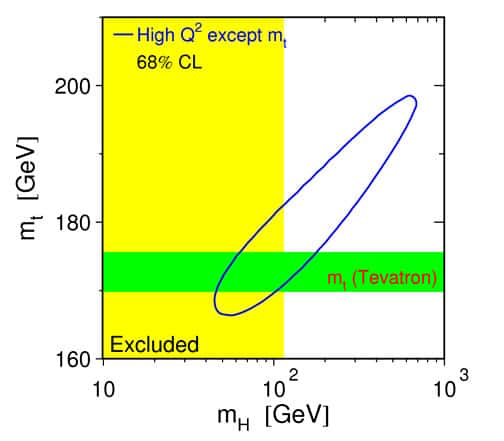
Fig. 18 : contrainte indirecte sur MH et Mtop (ellipse) comparée à la mesure directe de Mtop (bande horizontale). Les deux régions se recouvrent pour des valeurs de MH entre 50 et 200 GeV. La bande verticale est la région exclue par les recherches directes du boson de Higgs (voir paragraphe suivant).
C'est pourquoi, plutôt que de donner la valeur la plus probable de MH assortie de très grandes barres d'erreur, on préfère convertir le résultat en intervalle de masse exclu (à 95% de degré de confiance). On obtient ainsi :
MH
ce qui représente un progrès énorme par rapport à l'état des connaissances avant le LEP, puisque n'existait alors que la contrainte théorique MH avait l'énergie suffisante pour produire un boson de Higgs léger, typiquement jusqu'à 120 GeV de masse. Une telle particule aurait alors donné lieu à des états finals de collisions typiques, assez aisément identifiables parmi les millions d'états finals enregistrés. En effectuant une recherche directe de tels états finals dans la totalité des données accumulées, les quatre expériences LEP n'ont trouvé aucun signe d'un boson de Higgs sur une large gamme de masses, ce qui se traduit par une limite d'exclusion inférieure (à 95% de degré de confiance) de :
MH > 114,4 GeV
Là encore, il s'agit d'un progrès notable puisque la contrainte expérimentale avant le LEP s'établissait à MH a détecté une poignée d'états finals compatibles avec la production directe d'un boson de Higgs. L'un d'eux est représenté sur la Fig. 19. La masse du boson de Higgs reconstruite à partir des caractéristiques cinématiques de l'état final est de 114 ± 3 GeV. Un tel état final est également interprétable en terme de processus standard, sans production de boson de Higgs. Les probabilités qu'il soit dû à un boson de Higgs de masse 115 GeV (s) ou à un processus standard (b) ont pu être estimées et sont telles que : Ln(1+s/b) = 1,73. Les résultats combinés des recherches des quatre expériences ont ainsi révélé quelques états finals fortement compatibles avec l'hypothèse d'un signal de masse entre 115 et 118 GeV. Une compatibilitécompatibilité de 15 % avec l'hypothèse d'un boson de Higgs de 115 GeV a ainsi été estimée. Mais ces états finals sont également compatibles avec l'hypothèse d'une fluctuation du fond dû aux processus standard : une compatibilité de 9 % a été trouvée. La réponse du LEP sur l'existence d'un boson de Higgs de masse entre 115 et 118 GeV est donc ambiguë et ne pourra être affinée qu'avec l'aide des expériences auprès des accélérateurs qui ont pris ou vont prendre le relais du LEP.
Ces successeurs du LEP sont des collisionneurs hadroniques. Fonctionnant avec des faisceaux de protonsprotons ou d'antiprotonsantiprotons, ces machines sont moins pénalisées par le rayonnement de freinage que les machines circulaires à électrons, et peuvent donc monter beaucoup plus haut en énergie. Par contre, l'environnement expérimental y est beaucoup plus difficile, ne serait-ce que parce que les protons, au contraire des électrons, interagissent par interaction forteinteraction forte dont les sections efficaces sont très importantes et noient tout processus rare comme l'est la production du boson de Higgs. La mise en évidence d'un signal demande donc que les machines délivrent des taux de collisions élevés et requiert beaucoup de temps pour accumuler une statistique suffisante.
Le premier collisionneur hadronique à entrer en fonctionnement a été le Tevatron, qui a démarré une deuxième phase d'expérimentation en 2001. D'ici à 2009, le Tevatron devrait pouvoir explorer une gamme de masses allant de 100 à 180 GeV environ, les masses les plus basses étant les plus faciles à tester. En 2007, au CERNCERN, démarrera le LHCLHC, à plus haute énergie que le Tevatron. Sa sensibilité couvrira une gamme de masses plus étendue que celle du Tevatron, mais les masses inférieures à 130 GeV seront les plus difficiles à tester. Le LHC devrait donc donner une réponse en deux à trois ans pour des masses supérieures à cette valeur, puis revenir sur les plus basses masses ultérieurement.
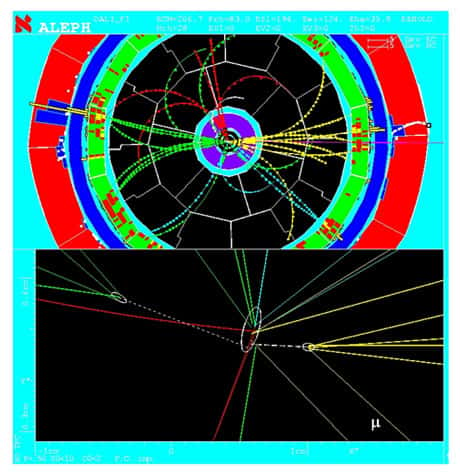
Fig. 19 : reconstitution graphique d'un état final de collision compatible avec la production d'une paire HZ, enregistré par ALEPH. La vue du haut en coupe transversale révèle quatre jets de particules, compatibles avec la production d'une paire HZ où chaque boson s'est désintégré en paire quark anti-quark. La vue du bas est une vue rapprochée de la région d'interaction entre électrons et positrons. Le point de collision est donné par l'ellipse centrale et les deux ellipses plus petites sont des vertex de désintégration de particules neutres, émises au point d'interaction mais qui se sont désintégrées à distance de ce point, comme on l'attend des particules formées à partir des quarks b (ou de leurs anti-particules). Cet état final contient donc une paire quark anti-quark et une paire quark b anti-quark b qui est la configuration la plus probable attendue dans le cas de la production d'une paire HZ.