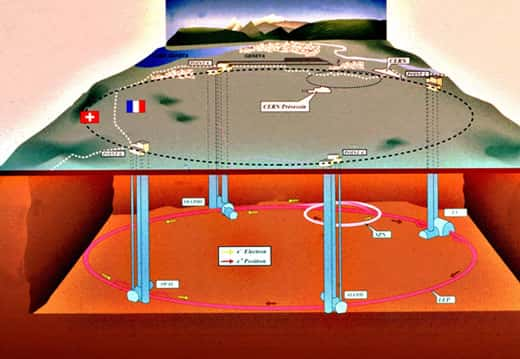
au sommaire
- À lire aussi
Le modèle standard de la physique des particules
Le cadre théorique de la physique des particules élémentaires est appelé modèle standard des interactions électromagnétique, faible et forte. Etabli au cours des années 60, le modèle standard rend compte de toutes les observations expérimentales accumulées jusqu'à ce jour. Comme nous le verrons par la suite, son contenu prédictif est fort, ce qui en fait une véritable théorie et non pas un modèle phénoménologique.
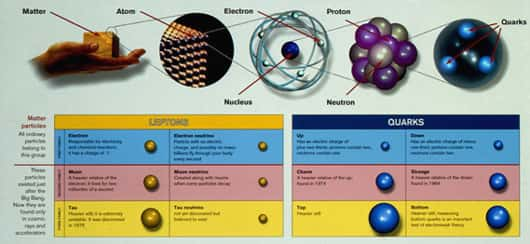
Les ingrédients du modèle standard sont en premier lieu les constituants élémentaires, c'est-à-dire non sécables (du moins avec nos moyens d'investigation actuels), de la matière. Au nombre de douze, les constituants élémentaires sont tous des fermions et se regroupent en trois familles, représentées sur la Fig. 12. La première famille permet de reconstituer toute la matière ordinaire : elle contient deux leptons, l'électronélectron et son neutrino associé νe, et deux quarksquarks, u et d, qui forment les nucléonsnucléons au sein des noyaux des atomesatomes. Rappelons que le νe est émis lors de la désintégration de certains noyaux radioactifs. Les deux autres familles ont la même structure en leptons et quarks, mais les constituants sont plus lourds d'une famille à la suivante. On ne les trouve que dans les rayons cosmiquesrayons cosmiques ou dans les états finals des collisions produites dans les accélérateurs.

Fig. 12 : table des douze constituants élémentaires de matière dont le modèle standard décrit les interactions. Les trois leptons chargés (électron, e-, muon, μ-, tau, τ- ) sont sensibles aux interactions électromagnétique et faible, les neutrinos (νe, νμ, ντ ) ne sont sensibles qu'à l'interaction faible et les six quarks (up, charm et top - ou u, c, t - de charge 2/3 et down, strange, bottom - ou d, s, b - de charge -1/3) sont sensibles aux trois interactions. En outre, chaque constituant élémentaire possède son anti-particule, de même masse et de nombres quantiques algébriques (comme la charge électrique) changés de signe.
La seconde famille est composée du muonmuon, de son neutrino associé νμ et des quarks squarks s et c. Enfin, la troisième famille est celle du lepton tau, de son neutrino associé ντ et des quarks b et t ou top. Le modèle standard ne prédit ni n'explique les valeurs exactes de certaines caractéristiques de ces constituants, comme la charge électrique ou la massemasse, dont la détermination revient à l'expérience. Par contre, le modèle standard a postulé l'existence des particules c, tau, ντ et quark topquark top avant leurs découvertes expérimentales. Celles-ci se sont d'ailleurs étalées sur plusieurs décennies et ne se sont conclues que récemment avec la mise en évidence expérimentale du quark top auprès du collisionneur Tevatron du laboratoire américain Fermilab en 1995, suivie par celle du ντ en 2000 toujours au Fermilab en expérience sur cible fixe cette fois. Les enjeux expérimentaux actuels consistent à préciser les propriétés des constituants les moins bien connus, à savoir le lepton tau, les neutrinosneutrinos et les quarks lourds c, b et top. Sur tous ces points, le LEPLEP a apporté des résultats importants.
Le second ingrédient du modèle standard est la description des trois interactions fondamentales qui interviennent au niveau microscopique : électromagnétismeélectromagnétisme, interactions faibleinteractions faible et forte. En postulant des propriétés d'invariance des interactions sous certaines lois de transformation (dites transformations de jauge locales), le modèle standard aboutit à la description en termes d'interactions propagées par des bosonsbosons médiateurs de spinspin 1 : le photonphoton, γ, pour l'interaction électromagnétique, les W+, W- et Z pour l'interaction faible, et huit gluonsgluons pour l'interaction forteinteraction forte. Des exemples de description de l'interaction entre un électron et un positronpositron sont donnés sur la Fig. 13. L'enjeu expérimental actuel est de préciser les caractéristiques des interactions faible et forte. Le LEP a là aussi permis des avancées significatives, en particulier sur l'interaction faible.
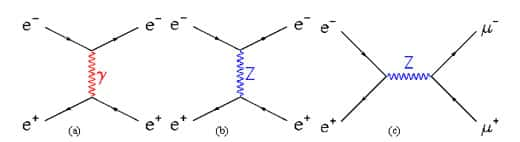
Fig. 13 : exemples d'interaction entre électron et positron : a) l'électron et le positron échangent un photon (interaction électromagnétique), b) l'électron et le positron échangent un Z (interaction faible), c) l'électron et le positron s'annihilent en un Z qui se désintègre en paire muon anti-muon (interaction faible).
Le troisième ingrédient du modèle standard est connu sous le nom de «brisure de la symétrie électrofaible». En effet, la description théorique des interactions suppose que les interactions électromagnétique et faible sont indiscernables à haute énergieénergie, autrement dit dans le passé de l'UniversUnivers. A un moment donné de l'évolution de ce dernier, cette symétrie électrofaible a été brisée, individualisant les deux interactions qui ont des propriétés différentes à basse énergie, donc aux échelles d'énergie accessibles actuellement à l'expérience. La brisure de la symétrie électrofaible est responsable de la génération des masses de toutes les particules, de matière ou médiatrices des interactions. Ainsi, le photon reste de masse nulle, expliquant la portée infinie de l'interaction électromagnétique. Les bosons W et Z acquièrent des masses, comme le requiert la portée finie de l'interaction faible. Contrairement au cas des particules de matière, le modèle standard prédit la valeur des masses du Z et des W :
MZ ~ 91 GeV MW ~ 80 GeV
A titre de comparaison, la masse d'un protonproton est équivalente à une énergie de 1 GeVGeV. Ces valeurs, ainsi que l'existence des bosons Z et W, ont reçu une confirmation expérimentale éclatante au début des années 80 au CERNCERN, par les expériences UA1 et UA2 du programme expérimental précédant celui du LEP. Cependant, cette confirmation n'était qu'une première étape. En effet, la découverte des bosons Z et W équivaut, pour l'interaction électrofaible, à la découverte des ondes herziennes pour l'interaction électromagnétique : il restait à mettre en évidence les effets quantiques fins équivalents à ceux révélés pour l'électromagnétisme (déplacements de Lamb, moments magnétiquesmoments magnétiques anormaux). C'est le LEP qui a permis de franchir ce pas.
Il reste enfin un dernier ingrédient de grande importance dans le modèle standard. Il s'agit du mécanisme exact de la brisure de la symétrie électrofaible, qu'on peut réaliser de multiples manières. L'une des possibilités, appelée «mécanisme de Higgs à un seul doubletdoublet de champs scalaires», revient à relier les masses des particules à leur couplage avec un boson de spin 0 dit «boson de Higgsboson de Higgs». C'est la piste privilégiée par le modèle standard. Cette solution, minimale puisqu'elle ne rajoute qu'une seule particule au spectrespectre déjà connu, est viable théoriquement et permet de prédire les propriétés du boson de Higgs comme ses modes de production et de désintégration, permettant ainsi de le rechercher expérimentalement. Par contre, la masse du boson de Higgs n'est pratiquement pas contrainte par la théorie, qui donne comme intervalle possible une fenêtrefenêtre entre 0 à 1000 GeV environ. Explorer la fenêtre entière requiert des moyens expérimentaux de très grande envergure (i.e. plusieurs programmes expérimentaux s'étalant sur plusieurs décennies) d'où la nécessité de rechercher tous les indices possibles sur le boson de Higgs. Il faut, de plus, faire de même pour tous les autres mécanismes de brisure. Sur ce thème aussi, le LEP a apporté une contribution significative.