La conjecture de Riemann

En 1859, dans un article à propos de l'étude de la fonction portant son nom, Bernhard RiemannBernhard Riemann glissa entre deux lignes une affirmation dont il jugea la démonstration superflue pour ce qu'il était en train de faire. Depuis, des générations de mathématiciensmathématiciens ont essayé, sans succès, de démontrer ce qu'il est convenu d'appeler la conjecture de Riemann, sans autre précision, tout le monde sait de quoi il s'agit.

Tout le monde ? Non, sans doute, alors il convient d'en dire un peu plus. La fonction étudiée par Riemann, notée , a comme toute fonction le droit de valoir exactement zéro pour certaines valeurs de son argument z -- on sait que c'est le cas quand z est un entier pair strictement négatif.

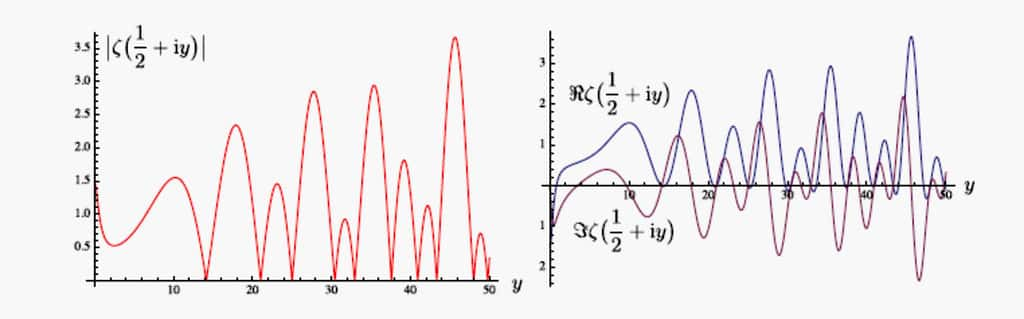
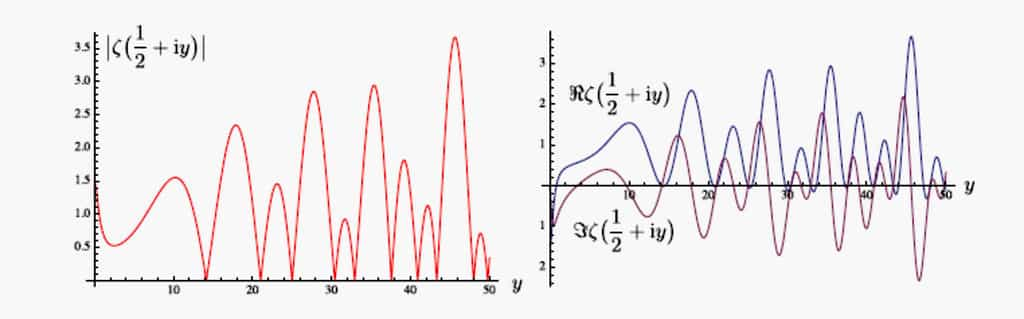
Module (à gauche) et parties réelle et imaginaire (à droite) de  quand y varie de 0 à 50. Tous les zéros de   indiqués ont 1/2 pour partie réelle. Et les autres ? © Claude Aslangul

L'histoire aurait pu s'arrêter là si l'on n'avait pas déjà su, grâce à Cauchy, Liouville et quelques autres, qu'une fonction donnée, initialement définie quand son argument est un nombre réel, peut être généralisée (sous certaines conditions) au cas où celui-ci est un nombre complexe ; on appelle cela « prolonger analytiquement ». Cette généralisation peut être faite pour , et Riemann s'est alors posé la question de savoir si, en dehors des valeurs paires négatives (appelées depuis zéros triviaux), la fonction  s'annulait ailleurs dans le plan complexe. On ne sait trop comment, il acquit la conviction, sans nous en donner la preuve, que ces valeurs existaient et, surtout, surtout, que ces nombres complexes remarquables avaient tous la même partie réelle, égale à 1/2 (la figure ci-dessus illustre cette affirmation, voir aussi la première note), donc tous situés sur une certaine droite verticale du plan complexe (ligne dite critique) -- et passa à ce qui le préoccupait sur l'instant.

Georg Friedrich Bernhard Riemann (1826-1866) était un mathématicien de génie. Ses contributions en analyse, géométrie et théorie des nombres sont légendaires : des espaces courbes à n dimensions jusqu'à la topologie, en passant par l'analyse complexe et la théorie de l'intégration. Il a anticipé la théorie de la relativité générale. © DP

Tous sur la ligne critique ? Drôle de question, pensera-t-on, et quelle importance ?

L'importance est considérable, notamment pour tenter de percer un mystère (encore un), celui de la répartition des nombres premiers, ceux que l'on ne peut diviser que par 1 (évidemment) et par eux-mêmes. Cette répartition est très bizarre : quand on commence à faire la liste de ces nombres, on découvre vite qu'elle a une structure très étrange, au sens par exemple où l'écart entre deux nombres premiers consécutifs ne semble obéir à aucune règle, sauf celle que l'intuition aurait tendance à designer comme le hasard (à condition de l'avoir préalablement défini sans ambiguïté !). On ne peut, à la main, aller bien loin dans une telle liste (c'est fastidieux), mais on peut quand même se rendre vite compte qu'en effet, la distance entre deux premiers qui se suivent a une variation très irrégulière.

C'est donc pour percer ce mystère que depuis des siècles, des mathématiciens déploient des trésors d'imagination et d'ingéniosité. Et c'est là que la fonction de Riemann entre en scène -- par des relations intraduisibles en langage ordinaire -- et que si la conjecture de Riemann est vraie, alors on aura mieux compris d'où vient cette répartition qui, aujourd'hui encore, garde presque tous ses secrets, même si des progrès ont pu être réalisés. Par exemple, Hardy a montré en 1914 que la fameuse droite critique contient une infinité de zéros -- mais cela ne veut pas dire qu'ils y sont tous. L'importance de la conjecture de Riemann peut aussi être mesurée au fait que le Clay Mathematical Institute en a fait l'un des sept problèmes du millénaire, dont la résolutionrésolution vaudrait à son auteur un peu plus qu'une poignée de dollars...

Godfrey Harold Hardy (1877–1947) était un mathématicien britannique de premier plan en théorie analytique des nombres. Les non-mathématiciens le connaissent surtout pour A Mathematician's Apology, son essai de 1940 sur l'esthétique des mathématiques, et son rôle de mentor à partir de 1914 avec le mathématicien indien de génie Srinivasa Ramanujan. © Wikipédia, DP

Cette conjecture est une nouvelle occasion de montrer du doigt ce qui distingue le mathématicien et le physicienphysicien quand ils utilisent pourtant le même langage. Précisons ce point. À l'heure actuelle, grâce à de puissants ordinateursordinateurs, il est prouvé que les 25 milliards de zéros les plus proches de l'axe réel sont tous sur la droite critique (voir deuxième note) ; en conséquence, le physicien qui travaille dans les bonnes unités (les bonnes échelles) ne manipulera pas usuellement des nombres aussi grands, de sorte que, s'il en a besoin pour progresser, il admettra que la conjecture de Riemann est prouvée et prendra appui dessus pour la suite de son travail. Bien évidemment, pour le mathématicien, la preuve en question n'en est pas une : 25 milliards ce n'est pas l'infini , et, avec justesse, il dira que rien n'est prouvé.

Qui a raison ? Tous les deux !

Notes

• Extraite de Claude AslangulClaude Aslangul, Des mathématiques pour les sciences (De Boeck, Bruxelles, 2011).
• Marcus du Sautoy, La symphonie des nombres premiers (Héloïse d'Ormesson, Paris, 2005).