Deuxième partie - Les problèmes actuels : la masse des neutrinos

La découverte des neutrinosneutrinos a ainsi été réalisée à la suite de l'étude de la désintégration du proton : n -> p + e(-) .

Dans le cas d'une désintégration en 2 corps du type a -> b1 + b2 , avec Va=0 , les équations de la relativité nous permettent d'établir la vitesse, l'énergie, et l'impulsion des produits.

En effet, en écrivant la conservation de l'énergie et de la quantité de mvt :

p1 + p2 = 0

E1 + E2 = ma.c²

On obtenait ainsi, dans la désintégration proposée, une énergie de 0,8 MeV pour l'électron, non conforme avec les mesures expérimentales. C'est ainsi qu'on a introduit le neutrino, la réaction réelle étant la suivante : n -> p + e(-) +antineutrino.elec (désintégration béta du neutronneutron).

Depuis la fin des années 70 a ainsi, grâce à l'étude de cette réaction , été possible la mise au point d'une méthode de calcul de massemasse.

Dans cette désintégration, on mesure avec un spectromètrespectromètre magnétique l'impulsion ou l'énergie des électrons qui s'échappent. Cette énergie présente l'allure d'un spectrespectre continu qui va de zéro à une valeur maximale égale à la différence d'énergie entre l'atomeatome père et l'atome fils. Et c'est là qu'intervient le neutrino : s'il a une masse, même si son impulsion est nulle au sortir de la désintégration , il faudra soustraire la valeur de cette masse à l'énergie maximale possible de l'électron. L'existence des neutrinos a d'ailleurs été postulée par Pauli pour que le principe de conservation de l'énergie soit vérifié lors de cette désintégration.

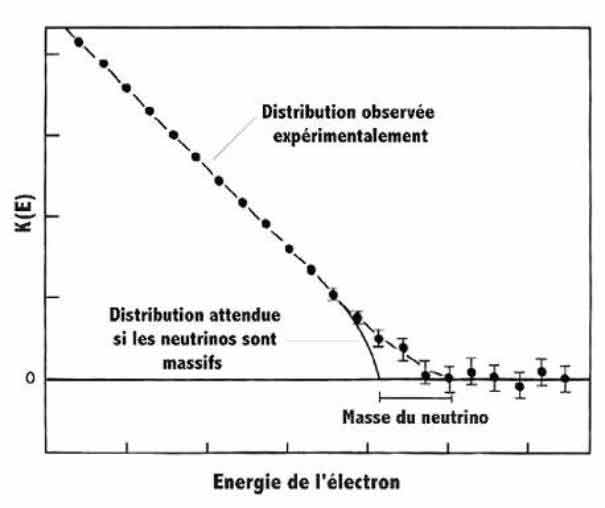
En 1936, le physicienphysicien américain Frank Kurie propose une représentation graphique simple du spectre de l'électron. Celle-ci est en fait obtenue en traçant la racine carrée du nombre d'événements divisé par le carré de l'impulsion, en fonction de l'énergie de l'électron. C'est cette représentation que l'on retrouve sur le document suivant :

Ainsi, si le neutrino a une masse , si faible soit-elle, la droite s'incurvera légèrement et interceptera l'axe un peu avant la valeur maximale possible.

La différence entre ces 2 valeurs représentera alors simplement la masse du neutrino. Cependant, cette belle méthode théorique se révèle parfois délicate à mettre en œuvre, pour 2 raisons majeures très simples :

* Tout d'abord, le point où la droite intercepte l'axe correspond à un nombre d'évènements très faibles : l'appareil devra donc fonctionner suffisamment longtemps, au risque de dérives systématiques.

*La seconde est que la précision des mesures doit évidemment être meilleure que la masse des neutrinos .. Or, le meilleur spectromètre a ses limites.

Grâce à cette méthode, on n'obtient donc à l'heure actuelle qu'une majoration de la masse des neutrinos. On obtient ainsi :

M(ue)

CONCLUSION

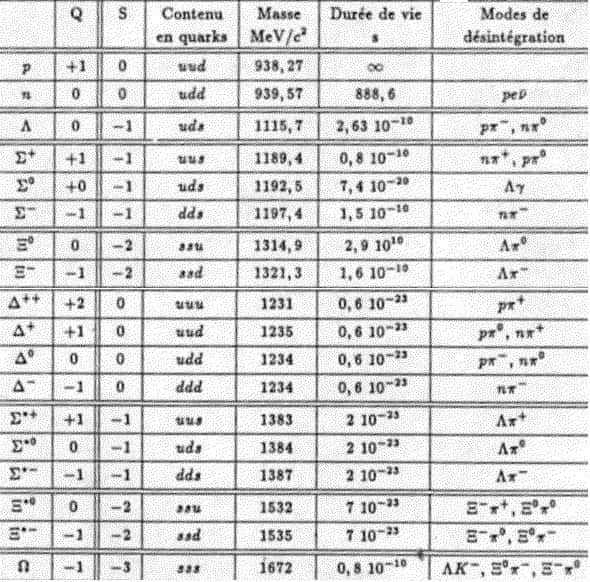
Le modèle Standardmodèle Standard actuel prévoit donc l'existence de 25 particules subatomiques (voir document 16), auxquelles il faudra peu t être bientôt ajouté l'hypothétique boson de Higgsboson de Higgs, quantum du champ de Higgs qui donne la masse des particules, et dont la découverte, sans cesse annoncée comme imminente, garantira le prix Nobel à son découvreur. Cependant, ce modèle est loin d'être un modèle fini et achevé. Si on a déjà soulevé le problème de la divisibilité des quarksquarks, d'autres interrogations apparaissent également dès que l'on s'attache à comparer les particules entre elles, laissant présager un changement profond dans le monde de la physiquephysique des particules. Ainsi, le parallèle facile à établir entre quarks et leptonsleptons a-t'il permis de supposer que ceux-ci ne seraient qu'une même famille de particules super-symétriques , où leptons et quarks, alors appelés s-leptons et s-quarks (s pour super-symétriques ) ne seraient que 2 représentations d'une même particule. Au delà de cette idée de particules super-symétriques se cache ainsi l'adversaire le plus en vogue du modèle Standard : la ( les : il y en a plusieurs versions) théorie (s) des cordes, annoncée comme le moyen d'unifier et de concilier les 2 grandes théories du 20ème siècle, à savoir relativité généralerelativité générale et la mécanique quantiquemécanique quantique. La plus prometteuse d'entre elle prévoit ainsi que notre universunivers serait en réalité composé de 11 dimensions, dont 7 enroulées sur elles même, et permet de décrire l'ensemble des particules élémentairesparticules élémentaires uniquement grâce à l'intervention de super-cordes vibrantes, de taille 10^-33 cm, et dont les différents modes de vibrationvibration donnerait l'ensemble des particules du modèle Standard.