La loi de Rayleigh-Jeans

Pour avoir une idée de ce qu'ont fait Rayleigh et Jeans, il faut prendre au sérieux le fait que le champ électromagnétique peut être considéré comme un système mécanique décrit par les équations de la mécanique analytique de Lagrange et Hamilton.

Considérons d'abord un système de points matériels de masses identiques et de coordonnées de positions x_n soumises à des forces. Selon les lois de Newton on pourra écrire (F désignant un ensemble d'expressions pour les forces):

On peut faire intervenir des quantités de mouvement p_n ce qui donnera les équations:

 

où l'on reconnaît déjà les équations de Hamiltonéquations de Hamilton-Jacobi de la mécanique dans un système de coordonnées donné.

Considérons maintenant une distribution continue de masses constituant une corde élastique dont les deux extrémités sont fixes et séparées par une distance l.

Il est bien connu que l'on peut décrire la propagation d'une onde sur cette corde avec l'équation suivante.

où a représente la vitessevitesse de propagation de cette onde.

Là aussi, le formalisme de Hamilton peut être appliqué et cette équation, qui est l'analogue de celle de Newton, mais pour une distribution continue de matièrematière, pourra s'écrire à l'aide d'équations rappelant celles d'Hamilton-Jacobi.

Les conditions aux limites sont les suivantes:

On peut alors décomposer la solution en séries de Fourier discrètes avec comme conditions initiales pour t=0

Maintenant, la solution générale dépendante du temps est

 

Or, en reportant dans l'équation d'ondes précédente on trouve:

 

Magiquement, l'état mécanique de la distribution continue de points matériels est en fait fixé par une série discréte de coordonnées mécaniques généralisées au sens de Hamilton. On reconnaît d'ailleurs un ensemble d'oscillateurs indépendants décrit par les équations de Hamilton-Jacobi ci-dessous:

 

avec 

L'évolution dans le temps de la mécanique de la corde est ainsi équivalente à la trajectoire d'un point de coordonnées (q_n,p_n) dans l'espace des phasesespace des phases habituel dans le cas du mouvement d'un système de points matériels.

L'énergieénergie totale E de la corde pourra alors s'écrire comme la somme des énergies d'une série d'oscillateurs harmoniques.

 

Maintenant, les équations de Maxwelléquations de Maxwell pour le champ électromagnétique dans une cavité aux parois parfaitement réfléchissantes peuvent donner lieu à une analyse tout à fait similaire à celle que l'on vient de faire. En considérant un cube dont la longueur des côtés est l, et en écrivant l'équation d'ondes pour le potentiel vecteur en utilisant la jauge de CoulombCoulomb (voir le lien dans le cours plus bas pour plus de détails), on montre que le champ électromagnétique est alors équivalent à un système d'oscillateurs harmoniques libres.

Si l'on considère le problème du rayonnement thermiquerayonnement thermique, on peut donc appliquer les formules établies pour un système mécanique, comme les particules d'un gazgaz, décrit par un ensemble discret de degrés de libertés dans l'espace des phases de ce système. C'est précisément ce que Rayleigh et Jeans ont fait.

Mais attention, du fait de la linéarité des équations de Maxwell, le rayonnement tout seul est bien équivalent à une série d'oscillateurs indépendants, ce qui fait que, normalement, ils ne peuvent échanger de l'énergie et en tant que tel, un équilibre thermique n'est pas possible!.

C'est le couplage avec les oscillateurs mécaniques des parois ou des objets matériels dans la cavité qui va assurer cette distribution de l'énergie et permettre d'atteindre l'équilibre thermodynamiquethermodynamique !

C'est en 1900, avant PlanckPlanck, que Lord Rayleigh présenta son analyse de la loi du rayonnement thermique. Toutefois, sa démonstration comportait quelques défauts qui furent corrigés en 1905 par James Jeans, son compatriote anglais, qui finira par être anobli en 1928.

Sir James Jeans (1877-1946).

Si on applique le théorèmethéorème d'équipartition de l'énergie à l'équilibre thermodynamique aux oscillateurs de la somme discrète précédente, chaque terme au carré prendra en moyenne la valeur

 

et l'on voit vite qu'un problème  se pose.

Maintenant, l'analyse exacte de Rayleigh et Jeans pour la densité d'énergie du rayonnement du corps noircorps noir va en fait faire intervenir une somme continue de termes dépendant de la fréquencefréquence. Si l'on fait intervenir cette densité d'énergie  on fera apparaître comme expression des termes à sommer/intégrer: 

 

On peut se ramener très simplement à la formule générale dérivée par Wien sur les bases de la compression adiabatiqueadiabatique du rayonnement dans une boîte avec des parois parfaitement réfléchissantes, car on peut  écrire:

Comme les physiciensphysiciens du XIX ième siècle l'avaient découvert, et comme on pouvait déjà le prévoir avec la somme discrète précédente, les choses se gâtent terriblement lorsqu'on cherche à intégrer cette relation pour calculer la quantité totale d'énergie lumineuse. On obtient en effet:

 

Une quantité manifestement infinie et montrant clairement l'échec de la physiquephysique classique puisqu'on s'est appuyé sur la charpentecharpente parfaitement établie de celle-ci, à savoir les équations de Maxwell et les principes de la thermodynamique statistique.

L'origine de la divergence de cette quantité n'est pas difficile à comprendre. On voit qu'au fur et à mesure qu'on s'élève en fréquence, et qu'on rejoint la région de l'ultravioletultraviolet et au-delà, la quantité d'énergie par intervalle de fréquence  croit en .

Toutefois, on peut remarquer que la loi de Rayleigh-Jeans fonctionne très bien pour les basses fréquences.

Pour les hautes fréquences, et en partie par analogieanalogie avec la loi de Maxwell-Boltzmann, Wien avait proposé en 1896 la loi phénoménologique suivante:  

      

qui là aussi marche très bien. Malgré tout, on est encore en face d'une contradiction grave au coeur des lois de la physique classique.

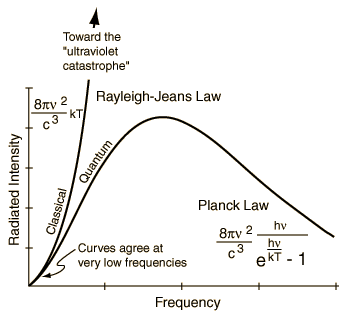
Les lois de Planck et Rayleigh-Jeans en fréquence. La loi de Planck, valide pour tout le spectre, résout le problème de la divergence infinie des calculs en physique classique pour la loi du corps noir ( Crédit : HyperPhysics (©C.R. Nave, 2006) ).

Quelques années plus tard, au XX ième siècle, le physicien Paul Ehrenfest exprimera de façon lapidaire l'apparition de ce problème à l'origine de la chute du monde clair et "rationnel" de la physique classique.

Il parlera de la "catastrophe ultraviolette", une formule qui connaîtra un grand succès.

La résolutionrésolution de ce problème viendra des travaux de Planck vers lesquels nous allons maintenant nous tourner.

Pour en savoir plus : cours de Claude Aslangul sur l'ancienne théorie des quanta.