Hawking et l'entropie des trous noirs

La première réaction d'Hawking à l'idée de Bekenstein a été que celle-ci était complètement fausse d'une part et qu'il allait le prouver d'autre part.

Stephen Hawking en visite à la Hong Kong University of Science and Technology (Crédit : Vincent Yu/AP). 

Certes, il y avait quand même deux résultats troublants que lui-même avait obtenus, notamment en collaboration avec James Bardeen et Brandon Carter, qui pouvaient servir d'arguments en faveur de la proposition de Bekenstein, mais cela ne pouvait certainement pas être autre chose qu'une analogieanalogie trompeuse.

Voyons voir pourquoi.

Par définition, un trou noir est une zone de l'espace-temps causalement déconnectée du reste de l'Univers. Pour être précis, il y a un horizon des événements entourant cette zone, laissant entrer dans celle-ci tout ce qui se présente mais interdisant ensuite à la matière et même à la lumièrelumière d'en sortir. Contrairement à ce que l'on croit souvent, ce n'est pas la présence d'une singularité où l'espace-temps s'anéantit qui définit un trou noir.

Les rayons lumineux possèdent une fréquencefréquence et une longueur d'ondelongueur d'onde, ils sont donc des règles et des horloges naturelles. Tout comme le comportement d'un fluide chargé définit l'état et la dynamique d'un champ électromagnétiquechamp électromagnétique en permettant de définir l'intensité d'un champ de forces électromagnétiques en un point de l'espace-temps et de visualiser avec les lignes de courants de ce fluide la dynamique du champ électromagnétique, de même, la dynamique et les propriétés des rayons de lumières sont les « traceurs » des propriétés et de la dynamique de l'espace-temps.

L'horizon des événements est alors défini par un ensemble de rayons lumineux générant la limite de cette zone d'où rien de ce qui entre ne peut sortir. La dynamique de la formation d'un trou noir et de sa réaction à des perturbations, sous l'effet de forces de maréeforces de marée extérieures ou lorsqu'un corps céleste y plonge par exemple, est alors équivalent à des théorèmesthéorèmes d'optique et de mécanique des fluides, mais ici pour les rayons de lumière générant l'horizon. En traitant leurs comportements à l'aide des outils de la topologie et de la géométrie différentielle, Hawking était parvenu à démontrer son fameux théorème de l'aire des trous noirs.

Celui-ci affirme que l'aire de la surface d'un trou noir, son horizon, ne peut que croître au cours du temps.

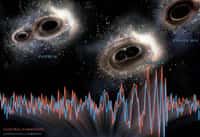
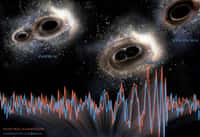
Aucun processus classique ne peut donc dissocier un trou noir en deux,  car la somme des aires des deux trous noirs aurait été inférieure au trou noir initial, et inversement, la fusionfusion de deux trous noirs doit donner un nouveau trou noir dont l'aire est supérieure à la somme des deux aires précédentes. Lorsqu'on connaît la relation entre l'aire A d'un trou noir et sa massemasse M (on a posé G=c=1):

 

il est facile de s'en convaincre, il suffit d'élever la somme des masses des trous noirs au carré.

Ce résultat était l'œuvre du seul Hawking, mais, lors de l'école de Houches sur les trous noirs, en collaboration avec Bardeen et Carter, la relation suivante valable pour un trou noir en rotation et chargé avait été démontrée.

 

Elle reliait les variations de la masse M d'un trou noir aux variations de la surface de son horizon, de son moment cinétiquemoment cinétique J et enfin de sa charge Q. L'analogie avec le premier principe de la thermodynamiquepremier principe de la thermodynamique exprimé par l'équationéquation suivante saute aux yeuxyeux.

Le terme de gauche étant celui de l'énergieénergie totale d'un système thermodynamique, il s'identifiera avec la masse du trou noir. Le premier terme de droite étant celui de l'échange de travail correspondant aux deux derniers termes de la relation précédente, il semble naturel pour aller jusqu'au bout de la logique de la connexion établie d'interpréter la surface du trou noir comme une mesure de l'entropieentropie. Cela l'est d'autant plus que le théorème de croissance de l'aire de Hawking exprime bien justement le second principe de la thermodynamiquesecond principe de la thermodynamique, avec la loi de la croissance de l'entropie.

Hawking, Bardeen et Carter refusèrent pourtant explicitement cette identification dans l'article publié en 1973 sous le titre « Les quatre lois de la mécanique des trous noirs ».

En effet, si l'aire d'un trou noir est une mesure de l'entropie de celui-ci, alors les principes de la thermodynamique ne laissent aucune échappatoire: un trou noir doit avoir une température et il doit rayonner. Comme de plus c'est un corps parfaitement absorbant, c'est un corps noircorps noir parfait au sens de Kirchhoff et il doit  émettre un rayonnement thermiquerayonnement thermique. Les lois de la thermodynamique entreraient donc en conflit avec les lois de la relativité généralerelativité générale interdisant à un trou noir de rayonner son énergie.

En couplant un trou noir avec un champ quantique de matière, tout comme l'atome de Bohratome de Bohr était couplé à un champ électromagnétique, Hawking a alors entrepris d'enterrer une fois pour toute la théorie de Bekenstein.

En fait, il s'interrogeait depuis quelques temps sur la production de mini-trous noirs dans l'Univers primordial. Dans les premiers instants de l'Univers la densité et la turbulenceturbulence du plasma de particules étaient telles que des trous noirs de masses bien inférieures à celle d'une étoileétoile pouvaient s'être formés et donner lieu à des reliques pouvant se comporter comme des atomes avec, au lieu d'un noyau, un mini-trou noir primordial chargé.

Il avait discuté de cela avec Zeldovitch et Starobinski à Moscou, et avait bénéficié de leurs lumières sur la théorie quantique des champs en espace-temps courbe. Notamment les applicationsapplications au phénomène de super-radiance des trous noir de Kerrtrous noir de Kerr en rotation, impliquant la création de particules au dépend de cette énergie de rotation.

La suite fait maintenant partie de l’histoire.

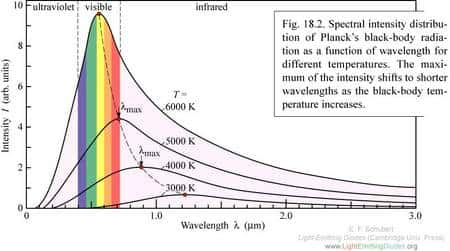
Hawking s'aperçu que ses calculs le conduisaient inévitablement à la conclusion qu'il voulait éviter : Bekenstein avait raison et la combinaison de la mécanique quantiquemécanique quantique avec les lois de la relativité générale se trouvait en harmonie complète avec la thermodynamique. Les trous noirs ne l'étaient pas complètement, ils émettaient un flux de particule aujourd'hui universellement connu sous le nom de rayonnement Hawking et le spectrespectre de ce rayonnement était précisément celui de PlanckPlanck.

Un résultat prodigieux montrant la cohérence incroyable des lois de la physiquephysique et confirmant une fois de plus la puissance des raisonnements thermodynamiques. Comme l'a fait remarquer Paul Davies, si l'on prend deux quelconques des trois théories précédentes on aboutit à des contradictions qui ne peuvent être levées qu'en introduisant la troisième théorie.

Entrer dans les détails de la théorie du rayonnement Hawking nous entraînerait trop loin mais basiquement, l'idée pour comprendre son origine est la suivante :

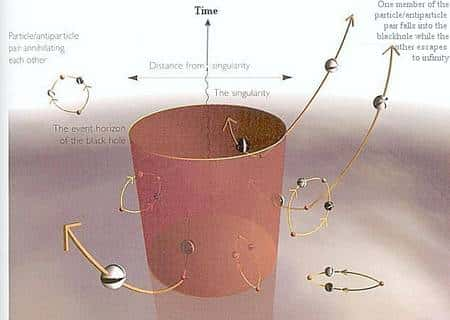
Le vide est perpétuellement agité par la création et la destruction de paires de particules, comme des électronsélectrons et des positronspositrons, des quarksquarks et des anti-quarks et même des photonsphotons qui sont leurs propres anti-particulesanti-particules. A l'aide de l'inégalité de Heisenberg temps-énergie, il est possible de violer la loi de la conservation de l'énergie pendant un temps inversement proportionnel à l'amplitude de cette violation.

Au voisinage d'un trou noir, les forces de marée, qui sont de plus en plus fortes avec la diminution de la taille d'un trou noir, sont susceptibles de séparer les paires de particules. Le travail de forces produit par cette séparationséparation fournit précisément l'énergie nécessaire pour créer les particules sans violer la conservation de l'énergie, mais au dépend de la masse du trou noir. Tous calculs faits, une des particules de la paire tombe dans le trou noir et laisse l'autre s'échapper à l'infini, loin de l'horizon.

( Crédit : http://universe-review.ca ).

Le résultat final est un rayonnement de corps noir comportant tous les types de particules possibles et dont la température s'élève, avec la luminositéluminosité, au fur et à mesure que le trou noir diminue et s'évapore. Bien sûr, la taille du trou noir diminuant, l'entropie de celui-ci baisse aussi et cela semble contredire le théorème d'Hawking et le second principe de la thermodynamique.

Il n'en est rien.

Le théorème d'Hawking ne vaut que par ses hypothèses qui font intervenir la physique classique et aucun effet quantique et en outre, comme le rayonnement du corps noir est très désordonné, il possède lui aussi une entropie. Celle-ci est d'ailleurs telle que le processus de formation puis d'évaporation d'un trou noir correspond bien au total à une croissance de l'entropie de l'Univers. Un résultat en plein accord avec les spéculations de Bekenstein et répondant à l'énigme soulevée par Wheeler.

Hawking pouvait maintenant donner une formulation exacte de la relation que Bekenstein avait conjecturée pour l'entropie d'un trou noir. Il s'agit de la formule suivante faisant intervenir les constantes les plus importantes de la physique, la vitesse de la lumièrevitesse de la lumière c, la constante de la gravitationconstante de la gravitation G et enfin celles de

Boltzmann k_b et de Planck.

De façon intéressante, on peut faire apparaître le carré de la longueur de Plancklongueur de Planck, l_p , en dénominateur de l'aire du trou noir A. Numériquement, l'entropie d'un trou noir de masse M est donnée par la formule suivante où la masse du SoleilSoleil apparaît au dénominateur dans sa notation standard.

La luminosité totale d'un trou noir de température TT et possédant une surface d'aire A va bien sûr être donnée par la loi de Stefan-Boltzmann que l'on a vue au début de ce dossier.

Avec comme valeur de la constante de Stefan

 

Sa température, quant à elle sera donnée par

 

Où l'on voit qu'un trou noir de masse solaire est particulièrement froid si on le compare à la température du rayonnement fossilerayonnement fossile.

Un trou noir de la masse de la Terre ne rayonnerait que comme un corps noir à une température de 0,02 K environ.

Enfin, plus un trou noir est petit moins il met de temps pour s'évaporer. Ramené à la masse de Planck M_p et au temps de Plancktemps de Planck t_p de 10^-44 s, le temps de vie d'un trou noir de masse M est donné par la formule suivante:

 

Un trou noir de la masse du Soleil mettrait ainsi environ 10⁶⁷ ans pour s'évaporer. Par contre, un trou noir de 961 KgKg aurait un rayon de Schwarzschildrayon de Schwarzschild de seulement 2,85 10^-24 m, serait aussi lumineux que le Soleil et aurait un temps de vie assez court. Malheureusement, jusqu'à présent, aucun mini trou noir primordial d'une masse de 10¹⁴ g et moins, susceptible de s'évaporer actuellement en émettant un rayonnement intense détectable, n'a été observé.

On pourra s'amuser à calculer plusieurs de ces nombres grâce au programme présent sur ce site

On peut être un peu plus précis en ce qui concerne les formules gouvernant l'évaporation d'un trou noir, en écrivant, par exemple, une formule pour le flux de particules bosoniques (comme les photons) rayonné par un TN. Posons pour simplifier les équations

 

Alors, la température et l'entropie d'un trou noir pourront s'écrire sous les formes suivantes:

    

et l'on aura la formule du schéma ci-dessous où l'on peut voir sous l'intégrale en facteur la loi de Planck pour un corps noir. Des formules plus complètes existent décrivant les flux de charges électriques, d'entropie et de moment cinétique émis avec différents types de particules par les trous noirs comme on pourra le constater dans cet article de Don Page

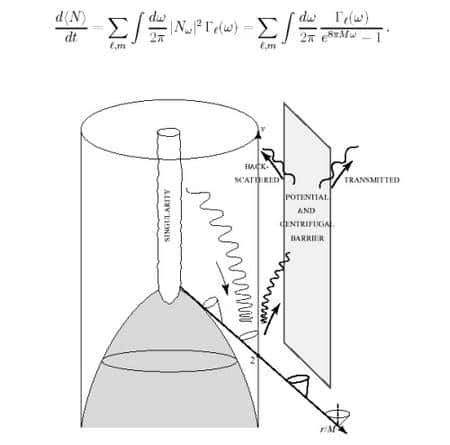
Diagramme d'espace-temps de la formation d'un trou noir par effondrement d'une étoile (en gris) passant sous l'horizon de  celui-ci (lignes verticales). Notez le basculement de l'inclinaison des cônes de lumière. Le rayonnement Hawking n'est cependant pas complètement thermique pour un observateur à l'infini car au delà de l'horizon existe une barrière de potentiel décrite par le facteur Gamma_l exprimant la réflexion d'une partie du rayonnement vers l'horizon (Crédit : Thibault Damour).

On pourra aussi trouver des renseignements sur les simulations numériquessimulations numériques de l'évaporation des trous noirs ici

On l'a dit, les détails de la dérivation du rayonnement Hawking ne sauraient être abordés ici. Le lecteur curieux et possédant un bon bagage en mécanique quantique et des bases en relativité générale pourra se reporter utilement aux cours de Gary Gibbons et Simon Ross. Les diagrammes d'espace-tempsdiagrammes d'espace-temps de la théorie des trous noirs y côtoient la théorie euclidienne de la gravitation quantiquegravitation quantique avec temps imaginaire et toute la machinerie des champs quantiques à haute température en espaces-temps courbes en liaison avec la théorie KMS.

Une très bonne référence, portant sur la thermodynamique des trous noirs, peut aussi se trouver dans le rapport de Paul Davies, l'un des maîtres de la théorie des champs quantiques en espace-temps courbes.