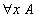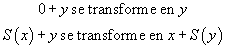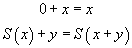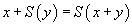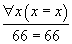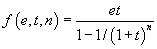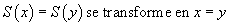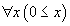
Démonstration automatique

En démonstration automatique, quelle que soit la méthode utilisée, on doit souvent comparer des propositions. Par exemple, si on a un axiome

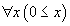
et qu'on cherche à démontrer la proposition

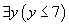
on compare les proposition 0 ≤ x et y ≥ 7 ce qui nous suggère d'utiliser l'axiome dans le cas x = 7 et de démontrer la conclusion dans le cas y = 0, et donc la démonstration

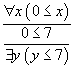
Ce problème de comparaison, qui s'appelle l'unification, ressemble beaucoup au filtrage. La seule différence est que dans le cas du filtrage les variables n'apparaissaient que dans l'un des termes comparés, alors qu'ici elles peuvent apparaître dans les deux.

Dans un système logique qui comprend des règles de déduction et des règles de calcul, les problèmes qui sont posés ne sont plus des problèmes d'unification ordinaires, mais des problèmes d'unification modulo les règles de calcul. C'est ce qu'on appelle l'unification équationnelle. L'algorithme pour l'unification simple, est essentiellement composé d'une règle de décomposition, qui transforme l'équationéquation

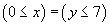
en le système

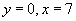
La comparaison des propositions

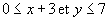
échoue : certes l'équation

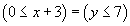
se simplifie en

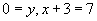
mais dans la seconde de ces équations le symbole de fonction est « + » dans l'un des termes et « S » dans l'autre, en substituant les variables, on ne peut pas changer ces symboles de fonction, et donc l'équation n'a pas de solution.

Si on compare maintenant ces deux termes modulo les règles de calcul, il y a une solution x = 4 qui apparaît. En effet, le terme 4 + 3 se réduit sur le terme 7. Comment peut-on trouver ce terme ? Outre la décomposition, on a une seconde règle, la surréduction, qui demande de substituer les variables par n'importe quel terme qui amène une réduction, par exemple dans le cas de l'équation x + 3 = 7 on substitue la variable x par le terme S(x'), le terme S(x')+3 se réduit alors en x'+4. En répétant cette opération, on obtient l'équation x''''+7 = 7, et on substitue x'''' par 0, ce qui donne x = 4.