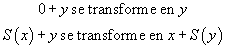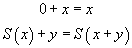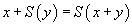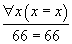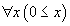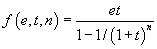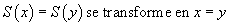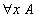
Propositions et règles

Un système formel est donné par deux choses : un ensemble P dont les éléments s'appellent des propositions et un ensemble de règles R, où une règle est donnée par un certain nombre de schémas de propositions dont l'un, la conclusion, est privilégié. Ces règles définissent un sous-ensemble D de P, qui est le plus petit ensemble clos par ces règles.

On peut, par exemple, donner le système formel constitué des cinq règles Suivantes : la première indique que de A ⇒ B et A, on peut déduire B, la deuxième que de

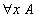
on peut déduire la proposition A dans laquelle on remplace la variable x par un terme quelconque, la troisième règle, sans prémisse, indique que Charles Martel est le père de Pépin le bref, la quatrième, sans prémisse également, indique que Pépin le bref est le père de Charlemagne et enfin la dernière, également sans prémisse, que le père du père de quelqu'un est son grand-père

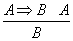
Si on veut, on peut appeler axiomes les règles sans prémisse, mais pour la simplicité de la définition, on peut simplement les considérer comme des règles ordinaires. Dans ce système, on peut démontrer un certain nombre de propositions, par exemple que Charles Martel est le grand-père de Charlemagne. En revanche, on ne peut pas démontrer que Charlemagne est le père de Charles Martel, ce qui est d'ailleurs faux. La proposition grand-père(Charlemagne, Charles Martel) est dans l'ensemble P, mais pas dans l'ensemble D.

Cette définition peut être critiquée de plusieurs façons, mais il me semble qu'on ne peut pas éviter d'en partir.
Une première critique est que tombent sous cette définition beaucoup de choses qu'on ne veut pas appeler logiques. Par exemple, si les propositions sont 0, 1, 2, 3, etc. et qu'on donne deux règles qui indiquent que 0 est démontrable sans prémisse et que si n est démontrable, alors n+5 l'est aussi, l'ensemble des propositions démontrables est 0, 5, 10, etc. On ne veut pas appeler logique un tel objet. Un autre exemple : on prend pour P les suites finies de lettres de l'alphabet. Puis on se donne les règles suivantes : un groupe nominal suivi d'un verbe transitif suivi d'un groupe nominal est une phrase, un article suivi d'un nom commun est un groupe nominal, le, l' et un sont des articles, aviateur et mouton sont des nom communs et dessine est un verbe transitif.

Ici encore, ces règles de grammaire peuvent être exprimées par un système formel. Chaque règle de grammaire se traduit par une règle de déduction, par exemple, la deuxième règle se traduit par

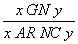
qui indique qu'on peut remplacer le symbole GN par la suite de symboles AR NC et ce dans n'importe quel contexte.

On a dans l'ensemble D la phrase « L'aviateur dessine un mouton », qui est vraie mais aussi la phrase « Le mouton dessine un aviateur » qui est fausse. C'est la grammaticalité et non la vérité qu'on définit ici. On ne veut donc pas appeler logique cet objet.

Une définition d'un ensemble D comme le plus petit sous-ensemble d'un ensemble P clos par un certain nombre de règles s'appelle une définition inductive. N'importe quelle définition inductiven'est pas une logique.
On peut donc restreindre cette définition en indiquant que les éléments de P doivent être des propositions assertoriques. On doit alors commencer par définir la notion de proposition assertorique. Une proposition assertorique est une chose susceptible d'être vraie, pour définir ce qu'est une proposition assertorique, il faut donc définir d'abord la notion de vérité, et si on pense que vrai est synonyme de démontrable dans une certaine logique, pour définir la notion de vérité, il faut d'abord définir celle de logique, ce qui nous ramène à notre point de départpoint de départ. Il faudrait donc définir l'une des trois notions : logique, proposition ou vérité sans utiliser les deux autres, et je ne vois pas comment le faire.

Cette critique consiste à dire que la définition d'une logique comme une définition inductive est trop vaste, elle capture trop de choses, elle capture certes les logiques comme celle ci-dessus mais aussi d'autres choses qui ne sont pas des logiques. On n'a donc pas suffisamment restreint la définition.

Je ne vais pas m'étendre sur ce type de critiques, car je pense que d'autres orateurs du séminaire auront des avis plus éclairés que le mien sur cette question. Je vais, en revanche, prendre le point de vue inverse : non seulement, cette définition capture trop de choses, mais également, elle n'en capture pas assez : une logique n'est pas toujours une définition inductive. La logique que j'ai donnée plus haut est une définition inductive, mais ce n'est pas le cas de toutes les logiques. Plus précisément, une logique n'est pas toujours uniquement une définition inductive, on retrouve toujours cette idée de règle de déduction, mais complétée par d'autres éléments.