au sommaire
Pommes de pin ou ananasananas, fleurs ou feuilles sur une tige, on retrouve des spirales similaires qui diffèrent légèrement de la spirale de Fibonacci. Le nombre d'or nous emporte toujours plus loin, au-delà de toutes limites.

Revenons aux photos de la page 2 et observons que l'ananas a 13 spires blanches et 8 bleues, pour le chardon c'est 89 et 55 et le tournesol 144 et 89.

Quatrième jeu, en forme d'observation : un exemple dans les spires qui fait rêver
Constatez que le nombre des spires dans un sens et le nombre des spires dans l'autre sens sont toujours deux nombres consécutifs de la suite classique de Fibonacci. Les observations sur d'autres plantes (à découvrir) vous donneront les mêmes résultats. Les nombres peuvent varier pour un même type de plante, par exemple des chardons avec 55 et 34 spires. Le nombre d'or est présent. La fin de l'observation devrait vous convaincre et même vous étonner.
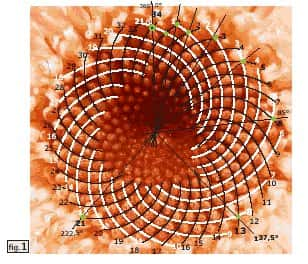
Regardez la photo qui montre la réalité de l'organisation des fleurons dans le cœur de cette fleur trouvée au hasard d'une marche. Ce cœur ne forme pas un vrai cercle, le creux du centre est désaxé, les spires de même couleur ne sont pas identiques... Essayez de trouver le centre ! Mais il y a 34 spires noires et 21 blanches.
Le nombre d'or, aspect essentiel du nombre
Tout ce qui vit sur Terre (et probablement dans l'UniversUnivers) dépend de son origine, de sa croissance et subit les évènements de son environnement. Deux fleurs ne seront jamais identiques et ne pourront pas correspondre à un modèle parfait mais il y a presque toujours des constantes : ici, les nombres de spires. Le dessin en figure 2 (ci-dessous) est tiré de « Nombre d'or, nature et œuvre humaine » (page 26 de l'ouvrage), c'est un cœur de marguerite de 21 et 13 spires.
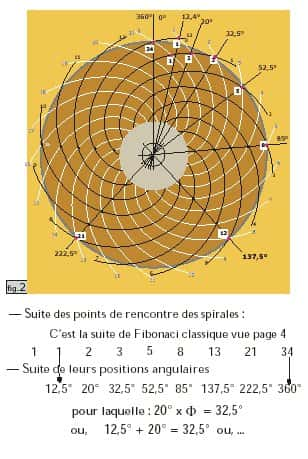
Repérez les points de rencontre des spires 1-2-3-5-8-13-21 noires avec les spires 1-2-3-5-8-13 blanches, ce qui génère les points de rencontre situés dans le carré blanc.
Lisez le texte sous la figure 2. Une nouvelle suite, par la position angulaire de ses points, engendre par la valeur de ses angles, une suite géométrique de Fibonacci dont Φ est la raison. Preuve que le nombre d'or est bien présent dans la nature.
Les points de rencontre des spires noires (34) et blanches (21) de la figure 1, quoique de nombres différents, forment les angles :
- 360°/Φ = 225,5°
- 360°/Φ2 = 137,5°
- 360°/Φ3 = 85°
- 360°/Φ4 = 52,5°
- 360°/Φ5 = 32,5°
- 360°/Φ6 = 20
Ces jeux s'achèvent, il reste beaucoup d'aspects du nombre d'or à découvrir, nous le verrons dans d'autres jeux.