au sommaire
- À lire aussi
Après l'adoption de la méthode axiomatique, le raisonnement a souvent été présenté comme l'unique outil à utiliser pour résoudre un problème mathématique. Dans le discours qu'ils ont tenu sur leur science, les mathématiciensmathématiciens n'ont quasiment plus accordé de place au calcul. Cela ne signifie pas que le calcul a disparu de la pratique mathématique : à toutes les époques, les mathématiciens ont proposé de nouveaux algorithmes pour résoudre systématiquement certains types de problèmes.
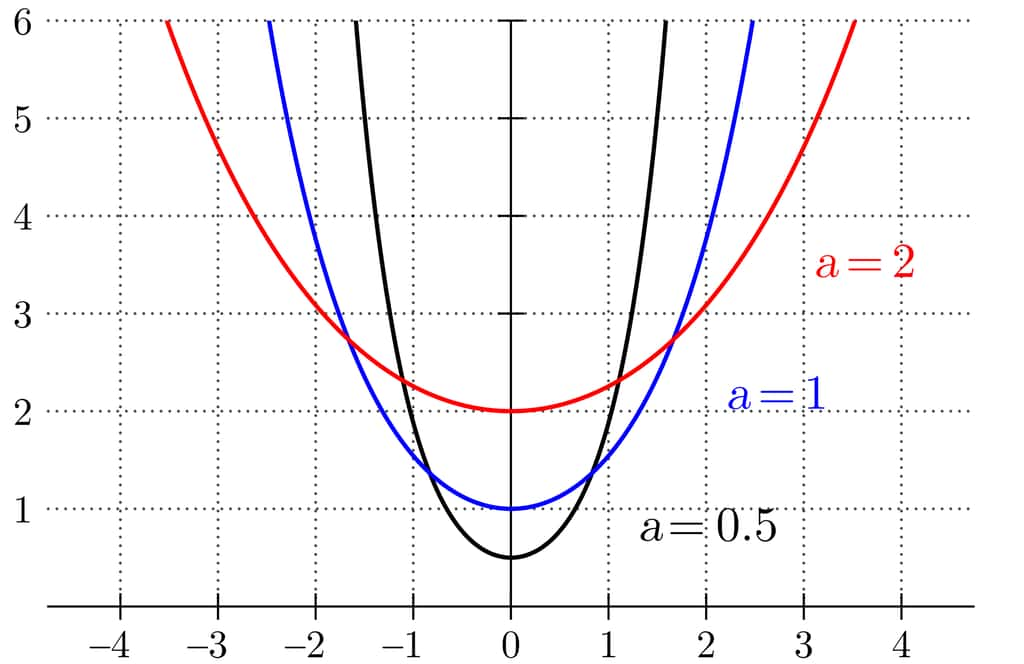
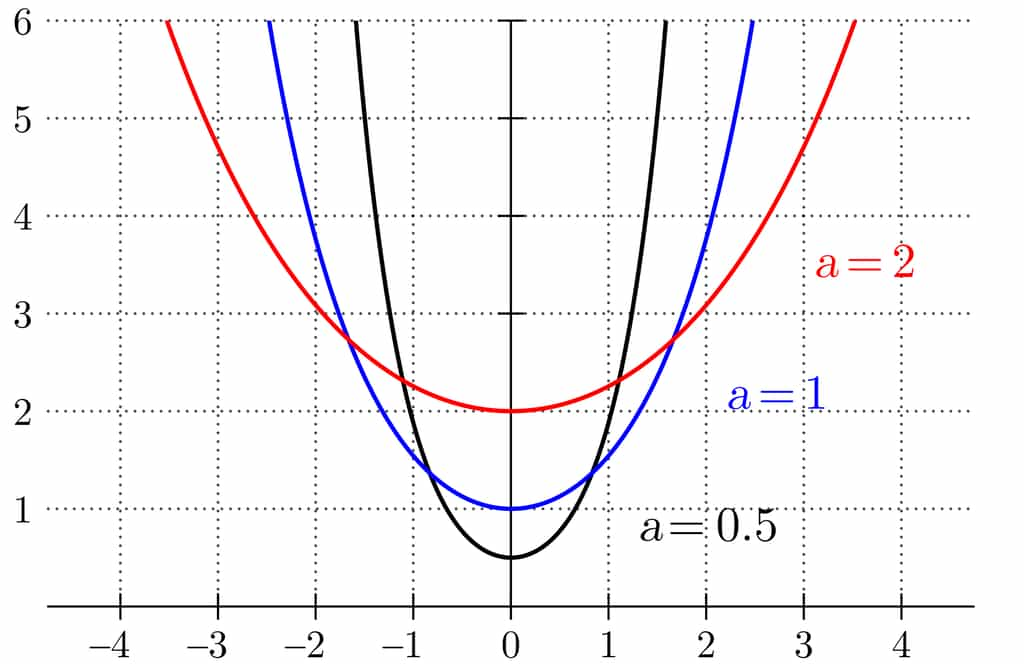
Trois courbes « chaînette ». © Geek3, wikimedia commons, CC 3.0
L'histoire des mathématiques a donc sa part lumineuse, celle des conjectures, des théorèmes et des démonstrations, et sa part d'ombre, celle des algorithmes.
Ce chapitre est consacré à trois moments de cette histoire. Ces trois moments, qui se situent à des époques différentes, nous amènent à discuter différentes questions.
Le premier nous amènera à nous interroger sur la manière dont peut se résoudre l'apparente contradiction entre le discours sur les mathématiques, qui accorde peu de place au calcul, et la pratique mathématique, qui lui en donne une si grande, ainsi que sur la façon dont la transition entre la préhistoire des mathématiques et les mathématiques grecques a pu s'opérer. Le deuxième nous amènera à nous interroger sur la part relative des héritages mésopotamiens et grecs dans les mathématiques médiévales. Le dernier, enfin, nous fera réfléchir sur la raison pour laquelle, alors que la géométrie de l'Antiquité était centrée sur un petit nombre de figures géométriques (le triangle, le cercle, la parabole...), de nombreuses nouvelles figures géométriques (la chaînette, la roulette...) sont apparues aux XVIIe siècle.