au sommaire
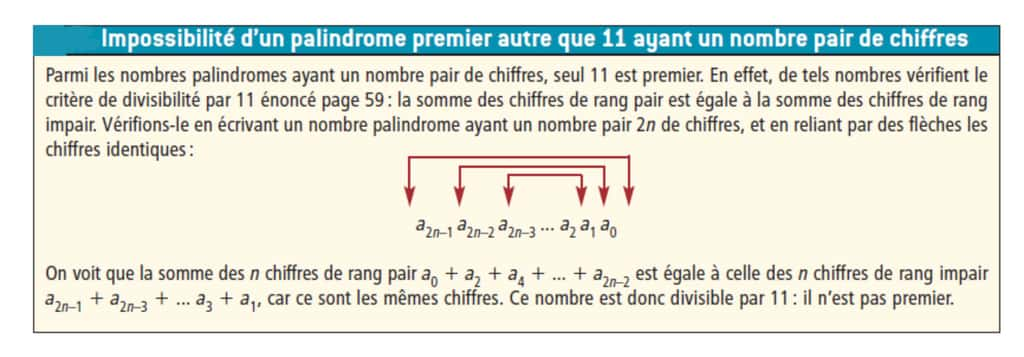
Le nombre 11 est le seul nombre palindrome à deux chiffres qui soit premier : en effet, un tel nombre est de la forme XX, donc multiple de 11. Plus généralement, à l'exception de 11, il n'existe aucun nombre premier palindrome ayant un nombre pair de chiffres.

En revanche, il existe 15 nombres premiers palindromes à trois chiffres : 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929. Notez qu'aucun n'a pour chiffre des centaines 2, 4, 5, 6 et 8 (en réfléchissant quelques secondes, vous comprendrez pourquoi).
Il existe 93 nombres premiers palindromes à cinq chiffres, et 668 à sept chiffres. Parmi ces derniers, mentionnons le quadruplet suivant (le chiffre central des palindromes figurera désormais en gras) :
1878781 -- 1879781 -- 1880881 -- 1881881
Cette suite est remarquable, car elle est composée de quatre nombres premiers palindromes pris dans quatre groupes consécutifs de 1.000 (c'est l'unique cas de ce type). Tous les nombres premiers palindromes de 11, 13 et 15 chiffres ont été calculés par l'amateur Martin Eibl. Le 9 juin 1998, ceux à 17 chiffres ont été calculés par Carlos Rivera. Ce Mexicain, passionné de nombres premiers, n'est pas un chercheur : il travaille dans l'industrie des céramiquescéramiques à Monterrey, mais il a trouvé le temps de mettre en place un site InternetInternet où il présente toutes sortes de propriétés et d'énigmes récréatives concernant les nombres premiers palindromes.
Exemples de nombres premiers palindromes
Voici quelques-unes des identités amusantes notées par Rivera.
Entre nombres premiers palindromes à trois chiffres :
101 + 131 + 151 = 383
Du même type, avec des palindromes premiers à cinq chiffres :
30103 + 30203 + 30403 = 90709
Plus impressionnante, entre palindromes premiers à 43 chiffres :
1000000000000002109952599012000000000000001 +
1000000000000002110000000112000000000000001 +
1000000000000002110025200112000000000000001 =
3000000000000006329977799236000000000000003
Cette égalité est la plus petite possible de sa catégorie (une somme de trois nombres premiers palindromes de 43 chiffres donnant un nombre premier palindrome de 43 chiffres). Toutefois, ce n'est qu'une égalité simple à côté de la suivante, où l'on a utilisé la notation (0)n pour désigner une suite de n zéros consécutifs. Il s'agit cette fois d'une égalité entre nombres premiers palindromes de 191 chiffres (notez que 191 est aussi un nombre premier palindrome) :
1(0)87132298010892231(0)871 +
1(0)87132300858003231(0)871 +
1(0)87132301111103231(0)871 =
3(0)87396899979998693(0)873
Toujours plus fort (ou plus absurde, selon les goûts), Rivera a découvert que le nombre premier palindrome 71317 s'écrit de trois façons différentes comme somme de nombres premiers consécutifs :
71317 = 2351 + 2357 + ... + 2579 + 2591
(29 nombres premiers consécutifs)
71317 = 10163 + 10169 + 10177 + 10181 + 10193 + 10211 + 10223
(sept nombres premiers consécutifs)
71317 = 14243 + 14249 + 14251 + 14281 + 14293
(cinq nombres premiers consécutifs)
Parmi les identités farfelues, les suivantes, découvertes au sujet du nombre premier palindrome 134757431, semblent miraculeuses. Ce nombre, qui mérite peut-être le titre de « nombre premier palindrome le plus intéressant », peut s'écrire de trois façons différentes comme somme de puissances des nombres 1, 2, 3, 4, 5, 6, 7, 8, 9, chacun pris une seule fois :
134757431 = 17 + 23 + 38 + 45 + 54 + 62 + 71 + 89 + 96
134757431 = 17 + 25 + 38 + 41 + 52 + 64 + 73 + 89 + 96
134757431 = 17 + 28 + 34 + 42 + 53 + 65 + 71 + 89 + 96
C'est le seul nombre qui possède cette propriété. Il existe - paraît-il - un autre nombre premier palindrome qu'on peut exprimer de deux façons différentes comme somme de puissances des nombres 1, 2, 3, 4, 5, 6, 7, 8, 9. Saurez-vous le retrouver ?