L’unicité de la décomposition en facteurs premiers

Ce théorème « clé » est ce qui nous manquait pour prouver enfin le résultat d'unicité de la décomposition en facteurs premiers. Le théorème de l'unicité de la décomposition en facteurs premiers s'énonce ainsi : tout nombre entier n supérieur à 1 s'écrit de manière unique (à l'ordre près) comme produit de nombres premiersnombres premiers.

Qu'est-ce que le théorème de l'unicité de la décomposition en facteurs premiers ? © Futura

Nous allons démontrer l'unicité de cette décomposition en effectuant un raisonnement par récurrence de type 2.

Le théorème est évidemment vrai pour n = 2. Considérons alors un nombre n supérieur à 2, et faisons l'hypothèse que tout nombre entier entre 2 et n - 1 possède un développement unique en facteurs premiers. Si nous parvenons à prouver que c'est aussi le cas pour n, le théorème sera démontré par récurrence. Afin de prouver que n se décompose de façon unique en un produit de facteurs premiers, on doit montrer que deux produits de facteurs premiers égaux à n sont nécessairement identiques à l'ordre près des facteurs. Notons q₁q₂...q_m et s₁s₂...s_p ces deux produits et considérons leurs premiers facteurs respectifs q₁ et s₁.

• Cas 1 : si q₁ = s₁, on simplifie de chaque côté de l'égalité : q₁q₂...q_m = s₁s₂...s_p qui devient : q₂...q_m = s₂...s_p

Les deux nouveaux produits q₂...q_m et s₂...s_p sont nécessairement égaux à un entier inférieur à n. On utilise alors l'hypothèse de récurrence (« tout nombre entier entre 2 et n - 1 possède un développement unique en facteurs premiers ») pour conclure que les décompositions q₂...q_m et s₂...s_p sont les mêmes à l'ordre près. Comme q₁ = s₁, les deux décompositions initiales q₁q₂...q_m et s₁s₂...s_p étaient donc, elles aussi, identiques à l'ordre près.

• Cas 2 : supposons que q₁ est différent de s₁.

L'égalité q₁q₂...q_m = s₁s₂...s_p signifie que le nombre premier q₁ divise le produit des deux nombres s₁ et (s₂...s_p). D'autre part, q₁ ne divise pas s₁, puisque deux nombres premiers différents n'ont, par définition, pas de facteurs communs autres que 1. En appliquant le théorème clé de l'arithmétique, on conclut que q₁, s'il ne divise pas s₁, divise s₂...s_p. Ce produit k = s₂...s_p est inférieur à n : par conséquent, l'hypothèse de récurrence s'applique (« tout nombre entier entre 2 et n - 1 possède un développement unique en facteurs premiers »), et l'on conclut que la décomposition s₂...s_p du nombre k est unique. Comme le nombre premier q₁ divise k, il est nécessairement l'un des facteurs premiers du produit s₂...s_p.

Une représentation des facteurs communs des nombres inférieurs à 100. © Belin

Comparer plusieurs décompositions

Reprenons alors l'égalité q₁q₂...q_m = s₁s₂...s_p pour la simplifier par q₁ de chaque côté. Les deux nouveaux produits de facteurs premiers sont égaux à un même nombre inférieur à n, et l'hypothèse de récurrence s'applique de nouveau, indiquant que les facteurs premiers sont (à l'ordre près) identiques de part et d'autre. Les deux décompositions initiales q₁q₂...q_m et s₁s₂...s_p étaient donc les mêmes à l'ordre près. En prouvant le cas 2 à la suite du cas 1, nous venons d'achever la démonstration de l'unicité.

Même si l'ordre des facteurs n'importe pas dans une décomposition en facteurs premiers, on doit être capable de s'y retrouver lorsqu'on compare plusieurs décompositions. Dorénavant, quand nous traiterons d'un nombre n ≥ 2 quelconque, nous écrirons sa décomposition en facteurs premiers en classant les nombres premiers par ordre croissant, par exemple p₁ = 2, p₂ = 3, p₃ = 3, etc., et en regroupant les facteurs identiques. Ainsi, la décomposition du nombre 120 s'écrit :
120 = 2 x 2 x 2 x 3 x 5 = 2³ x 3¹ x 5¹

L'exposant d'un nombre premier p_i, facteur d'un nombre n, est nommé la multiplicité de p_i dans la décomposition de n.

Nous serons parfois amenés à écrire des multiplicités nulles. Une telle notation est utile quand on doit traiter simultanément plusieurs nombres, car on fait alors apparaître les mêmes facteurs premiers dans chaque décomposition ; par exemple, 20 = 2² x 3⁰ x 5¹ x 11⁰ et 33 = 2⁰ x 3¹ x 5⁰ x 11¹. Cette notation permet aussi d'écrire n'importe quel nombre n sous la forme :

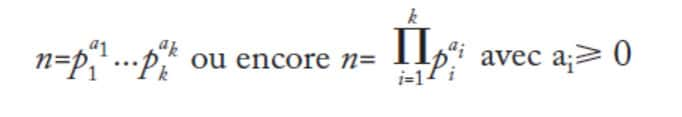
(le symbole Π représente le produit) où les p_i correspondent à la suite des nombres premiers p₁ = 2, p₂ = 3, p₃ = 5, p₄ = 7, p₅ = 11, p₆ = 13, etc. Dans ce produit, les nombres premiers qui ne sont pas facteurs du nombre considéré reçoivent une multiplicité a_i nulle.

Certains nombres premiers remarquables permettent de réaliser des tours amusants sans difficulté. © Belin

En affirmant l'existence et l'unicité de la décomposition en facteurs premiers, le théorème fondamental de l’arithmétique permet d'énoncer et de démontrer très facilement.