Le crible d’Ératosthène

Pour connaître en une seule fois un grand nombre de nombres premiers consécutifs et pas trop grands (par exemple inférieurs à un milliard), on dispose d'une méthode vieille de plus de 2.000 ans : le crible d'ÉratosthèneÉratosthène.

Ératosthène enseignant à Alexandrie. © Musée des Beaux-Arts de Montréal, Wikimedia Commons, DP

Le crible d'Ératosthène consiste à écrire tous les nombres d'un intervalle donné, puis à éliminer méthodiquement les multiples des nombres premiers successifs déjà connus, en s'arrêtant à la racine carrée de la borne supérieure de l'intervalle. Les nombres restants sont les nombres premiers de l'intervalle. C'est une bonne méthode, souvent utilisée pour constituer des listes de nombres premiers successifs, soit entre 2 et n (cas usuel), soit même entre deux bornes quelconques A et B.

Algorithme du crible d’Ératosthène

Pour connaître tous les nombres premiers jusqu'à n :

• écrire tous les entiers de 2 jusqu'à n ;
• enlever tous les multiples de 2 sauf 2 ;
• repérer le premier nombre plus grand que 2 encore présent, c'est-à-dire 3, et enlever tous les multiples de 3 sauf 3 ;
• repérer le premier nombre plus grand que 3 encore présent, c'est-à-dire 5, et enlever tous les multiples de 5 sauf 5 ;
• etc.
• s'arrêter dès qu'on a atteint la racine carrée de n ;
• ce qui reste est la table des nombres premiers jusqu'à n.

Les limites de cette méthode sont, là encore, fixées par l'espace mémoire dont on dispose et qui empêche de considérer des ensembles de nombres trop grands. On a récemment utilisé le crible pour compter exactement les nombres premiers jumeaux (c'est-à-dire séparés de deux unités, comme 11 et 13) inférieurs à 10¹⁵, ainsi que pour étudier les écarts entre les nombres premiers. À cette occasion, on a appliqué le crible par tranches de 10¹⁰ : après avoir sauvé les informations désirées, on effaçait les résultats du calcul de chacune de 100.000 tranches (sauf la première) afin de traiter la suivante.

Le crible d'Ératosthène appliqué aux 400 premiers entiers, disposés en un pavé de 20 x 20 (à gauche). Les nombres pairs se terminant par un chiffre pair, toutes les colonnes de numéro pair sont vides (à part la première, qui contient 2). On remarque aussi des « trouées » de trois colonnes : elles correspondent à l'élimination des multiples de cinq qui se terminent par cinq, flanqués de deux colonnes de nombres paires, vides elles aussi. Les multiples de deux et cinq, caractérisés par leur dernier chiffre, sont les seuls à se répartir ainsi en colonnes. Le reste du motif a l'air désordonné. À droite, le crible d'Ératosthène appliqué aux 10.000 premiers entiers, disposés en un pavé de 100 x 100. On retrouve l'alternance d'une colonne vide sur deux, correspondant aux nombres pairs, et les trouées de trois colonnes vides de dix en dix. © Belin

Si, au lieu de les effacer, on avait sauvé à chaque fois les résultats intermédiaires, on aurait disposé de la table des 29.844.570.422.669 nombres premiers inférieurs à 10¹⁵. Le stockage de cette table aurait nécessité une mémoire de 20.10¹² octetsoctets, soit plus de 30.000 CD-ROMCD-ROM de 650 mégaoctets chacun, ou plus de 1.000 DVDDVD double face double couche de 17 gigaoctets chacun. Il est clair que pour connaître des nombres premiers de 20 chiffres ou plus ou pour factoriser des entiers de cette taille, le crible d'Ératosthène ne convient pas. Dans 100 ans, si les progrès techniques se poursuivent à la vitesse d'un doublement tous les 18 mois, on ira au mieux jusqu'à 10⁴⁰ avec le crible.

Exemple de crible d’Ératosthène pour les nombres premiers inférieurs à 100. Il n’est pas nécessaire d’examiner les multiples au-delà de ceux de sept. © Belin

Constituer de très grandes tables de nombres premiers est impossible - à cause de la mémoire nécessaire - et inutile, car on dispose d'autres méthodes pour connaître la primalité : il vaut mieux recalculer que stocker. Aujourd'hui, on sait tester si un nombre entier quelconque de 100 chiffres est premier, alors qu'un ordinateurordinateur de la taille du Système solaire ne suffirait pas à stocker la table de tous les nombres premiers inférieurs à 10¹⁰⁰.

Spirale d'Ulam pour les entiers de 1 à 10.000 (à gauche). Spirale d'Ulam pour les entiers de 1 à 100.000 (à droite). © Belin

Les représentations du crible d'Ératosthène font naître également la question de la répartition des nombres premiers. Dans le processus d'élimination des multiples des nombres premiers successifs, on procède à des coupes régulières dans le massif des nombres entiers. Par exemple, quand on dispose les nombres entiers d'un intervalle en pavé, l'élimination des nombres pairs fait apparaître des colonnes vides de deux en deux, et, de façon générale, l'élimination des multiples du nombre premier p vide les cases de p en p.

Assistant à une conférence ennuyeuse lors d'un congrès en 1963, le mathématicien Stanislaw Ulam griffonna une spirale de nombres entiers en noircissant les nombres premiers. À sa grande surprise, il vit apparaître de nombreux alignements obliques. Ces alignements correspondent à des formules du type an² + bn + c, qui, sans qu'on sache bien expliquer pourquoi, génèrent parfois une proportion importante de nombres premiers. Par exemple, la formule d'Euler, f(n) = n² - n + 41, donne des nombres premiers pour toutes les valeurs de n entre 0 et 40. © DR

Toutefois, la combinaison de ces coupes régulières fait apparaître un motif sans régularité évidente, mis à part les colonnes vides de nombres pairs et celles des nombres qui se terminent par cinq.

On peut dessiner des spirales d'Ulam de toutes tailles, par exemple de 1 à 1.000. On peut aussi les centrer sur un autre nombre que 1. © Belin

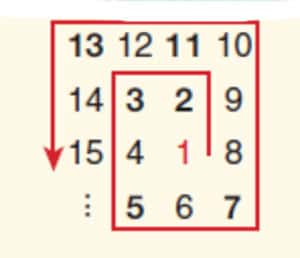
Une autre représentation des nombres premiers fait toutefois apparaître des structures supplémentaires : il s'agit de la spirale d'Ulam, découverte par le mathématicien Stanislaw Ulam. Elle consiste à disposer les entiers successifs, en général à partir de 1, en une spirale croissant vers l'extérieur, où l'on souligne les nombres premiers. Des lignes diagonales riches en nombres premiers, encore mal comprises, apparaissent alors.