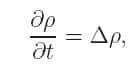au sommaire
- À lire aussi
Comme on le sait bien, les progrès scientifiques sont largement imprédictibles. Vers la fin des années 1980, trois chercheurs vont indépendamment contribuer à bouleverser de fond en comble notre vision du transport optimal : Yann Brenier (Paris), Mike Cullen (Reading), John Mather (Princeton).
Exit les problèmes d'ingénierie ou d'économie! Brenier, Cullen et Mather montrent que le paradigme du transport optimal se cache dans de nombreux phénomènes physiques bien connus. Pour Brenier, c'est la mécanique des fluides incompressibles et non visqueux. Faites couler de l'eau dans votre évierévier, examinez les remous qui se forment et se défont : avec une bonne approximation, on peut considérer qu'ils sont régis par l'équation de Navier-Stokes incompressible, qui décrit des fluides incompressibles et visqueux. Si l'on oublie l'effet de la viscosité, on trouve l'équation d'Euler, qui s'applique dans des situations où la viscosité est négligeable (comme pour des superfluides ou certains écoulements météorologiques).
A priori plus simple puisque ne tenant pas compte de la viscosité, l'équation d'Euler (dont nous fêtions récemment les 250 ans !) est l'un des mystères les plus respectables de toutes les mathématiques : nul ne sait si elle admet toujours une solution ! (ou du moins une solution physiquement pertinente... je n'en dirai pas plus, cela nous entraînerait beaucoup trop loin). Spécialiste de la théorie mathématique de la mécanique des fluides, Brenier montrait, dans un article remarquable, que certaines solutions pouvaient être construites au moyen d'une procédure complexe faisant intervenir le transport optimal comme outil clé.
A la même époque, Mike Cullen, un météorologuemétéorologue avec un goût prononcé pour les mathématiques, trouvait lui aussi un lien entre le transport optimal et la mécanique des fluides -- cette fois en météorologiemétéorologie ! Le transport optimal, montre-t-il, joue un rôle central dans les équations semi-géostrophiques, utilisées dans des simulations météorologiques pour décrire des "fronts''.
Présentés ainsi, ces liens semblent incompréhensibles : quel rapport entre l'entrepreneur qui veut minimiser le coût de transport, entre les unités de production et de consommation, et les molécules de fluide qui se pressent les unes les autres dans un écoulement atmosphérique ?
La seule façon de convaincre le lecteur sans ambiguïté serait d'écrire des équations... C'est en fait l'un des grands bonheurs des mathématiciensmathématiciens, que de pouvoir utiliser le langage abstrait et précis des mathématiques pour faire le lien entre deux problèmes concrets différents.
Hélas, ces équations ne seront compréhensibles que de personnes ayant un solidesolide bagage scientifique. Pour l'instant, je me contenterai de demander au lecteur de remplacer en pensée les paniers de croissants par de petites molécules dans l'atmosphèreatmosphère, et d'admettre que les équations qui régissent ces problèmes ont des points communs bien cachés.
Je ne parlerai pas non plus des contributions de John Mather, qui elles concernent une branche complètement différente de la physique : l'étude des systèmes dynamiques (équations différentielles apparaissant en mécanique classique, comme dans l'étude du pendule oscillant).
Il fallut une dizaine d'années à la communauté mathématique pour bien digérer ces travaux --- et encore, tout n'est pas parfaitement clair aujourd'hui ! C'est une chose de mettre le doigt sur une découverte importante, c'est autre chose de pouvoir l'expliquer complètement, et en cela les mathématiques se comportent comme les autres sciences. En tout cas, le transport optimal était bien parti pour une nouvelle jeunesse, avec une vitalité que personne n'aurait pu prédire.