Pi : le rapport de la circonférence au diamètre

Il y a bien longtemps les géomètresgéomètres comprirent que la longueur de la circonférence d'un cercle valait environ trois fois son diamètre.

Pi. © Geralt - Domaine public

Dans le papyrus Rhind, PiPi était égal au carré de 16/9, soit 3,16049. Les Babyloniens avaient calculé que le rapport était légèrement supérieur à 3 et utilisaient 3 1/8, très proche de l'approximation que l'on donne dans les livres d'école, 3 1/7. Au III^e siècle de notre ère, le mathématicienmathématicien chinois Liu Hui inscrivit un polygone de 292 côtés dans un cercle, puis un autre polygone de 3.072 côtés pour calculer Pi. Il trouva 3,141024.

Si le diamètre du cercle est 1, sa circonférence est π (Pi). © John Reid & Arpad Horvath licence Creative Commons paternité – partage à l’identique 3.0 (non transposée)

Calcul de Pi : la méthode d'Archimède

ArchimèdeArchimède montra que π (Pi)) était compris entre 3 10/71 et 3 1/7. Comme nous l'avons vu, les géomètres grecs étaient compétents pour construire des polygones en utilisant le compas et la règle. Archimède calculait la circonférence d'un cercle en l'insérant entre un polygone inscrit (dont les sommets étaient sur le cercle) et un polygone circonscrit (dont les côtés étaient tangents au cercle). Il est facile de commencer le calcul avec des hexagones inscrits et circonscrits.

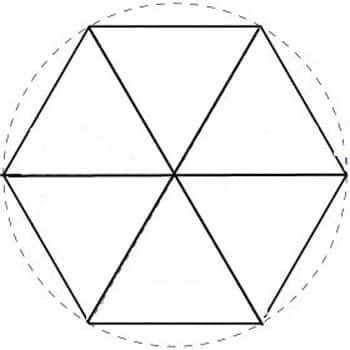
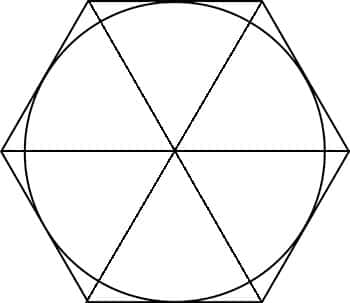
Méthode d'Archimède pour calculer la circonférence d'un cercle : placer ce cercle dans un polygone inscrit puis dans un polygone circonscrit. © DR

Si le rayon d'un cercle est égal à une unité, alors le périmètre de l'hexagone inscrit est égal à 6 ; cela fait que la circonférence est supérieure à trois fois le diamètre. Nous utiliserons le théorème de Pythagore pour calculer la longueur du côté de l'hexagone circonscrit. Si la longueur du côté de cet hexagone est R, le fait qu'il touche le cercle à la moitié d'un côté nous permet de tracer le triangle suivant :

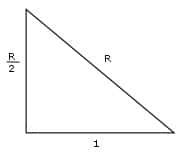
Utilisation du théorème de Pythagore

R² = (R/2)² + 1²
R² =(R²/4) + 1
(3/4) * R² = 1
R² = 4/3
R = 2 / √3

R vaut environ 1,15. Aussi le périmètre de l'hexagone circonscrit vaut un peu moins que 7, soit 3 fois et demi le diamètre du cercle.

Archimède connaissait la méthode pour doubler le nombre des côtés d'un polygone régulier et, en construisant des polygones de plus en plus grands, il calculait la valeur de π. Ainsi il utilisa des polygones à 12, 24, 48 et finalement à 96 côtés pour améliorer son approximation de π. Il utilisa une méthode similaire pour calculer l'aire d'un cercle.

Le calcul moderne de Pi

Avec des programmes adaptés, les spécialistes calculent plusieurs milliards de décimales de π. Comme Pi est un nombre irrationnel, nous ne connaîtrons jamais entièrement sa valeur.

Les experts en calcul mental retiennent des milliers de décimales de π. Le Chinois Chao Lu détient le record avec 67.890 décimales de Pi, qu'il a récitées en novembre 2005 au cours d'une séance de 24 heures et 4 minutes. Si vous êtes moins ambitieux, vous vous souviendrez des premières décimales de Pi en retenant la phrase : Que j'aime à faire connaître ce nombre utile aux sages. Les nombres de lettres des différents mots indiquent les décimales, en ne comptant pas l'apostrophe : 3,1415926535.