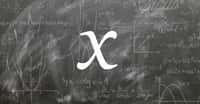Les objets mathématiques

Qu'est-ce qu'un objet mathématique, vous demandez-vous ? Un objet mathématique se distingue d'un objet réel en ce qu'il est idéal, c'est-à-dire parfait.

Fleur fractale. © BarbaraALane - Domaine public

Les fractales sont des objets mathématiques étudiés par la géométrie. © Solkoll Domaine public

Symétrie : la distinction entre le réel et l'idéal

Dans le monde réel, un papillon n'est jamais parfaitement symétrique (un examen approfondi révélera de petits détails discordants sur les ailes). Même si vous le dessinez avec grand soin, un agrandissement révélera toujours des défauts de symétrie minuscules. Dans la vie courante, ces imperfections se remarquent à peine, mais elles importent au mathématicienmathématicien qui vit dans un monde parfait. La distinction entre le réel et l'idéal est une des plus importantes notions qu'EuclideEuclide nous a léguées. La géométrie traite d'objets mathématiques idéaux, tels que des points, des droites, des polygones, des polyèdres et aussi des fractales qu'Euclide ne connaissait pas. Dans le cas du papillon mathématique, l'opération mathématique qui préserve son aspect est la réflexion : vous ne pouvez déterminer si vous regardez le papillon original ou sa réflexion. Similairement la rotation du dessin de cœurs de pommes conserve son apparence par réflexion.

La symétrie mathématique 

Élargissons le concept de symétrie. Prenons un triangle et l'opération mathématique qui consiste à le dilater ou à le contracter. Dans le langage de tous les jours, ces différentes versions du triangle ne sont pas considérées comme symétriques. Mais, comme l'opération de dilatationdilatation (et de contraction) conserve certaines propriétés du triangle par exemple la valeur des angles ou le rapport des côtés, cette dilatation est une symétrie mathématique.

Les triangles sont symétriques dans l'opération de dilatation en ce qui concerne les angles et le rapport des côtés. Nous obtenons plusieurs images d'un même triangle en le déplaçant dans le plan (sans le tourner) et cette opération est dénommée translation ; c'est aussi une symétrie.

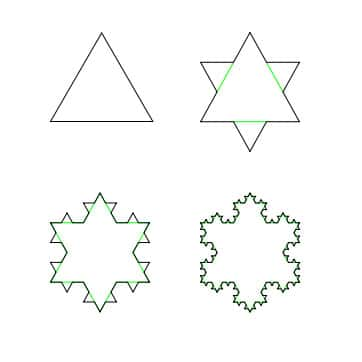
Le problème du flocon de neige de von Koch, est que l'on ne peut définir avec une absolue précision son aire. © Wxs licence Creative Commons paternité – partage à l’identique 3.0 (non transposée).

Symétrie : rotation, dilatation, contraction...

Ces symétries de base - la réflexion, la rotation, la dilatation, la contraction, la translation et toutes leurs combinaisons - sont la base de la géométrie euclidienne, c'est-à-dire la géométrie des figures planes. Les figures planes sont représentées à deux dimensions et étendues à trois dimensions par des plans verticaux. Ces symétries sont tout à fait intéressantes et étudiées à l'école. Les « faits » que nous apprenons, par exemple que la somme des angles d'un triangle est toujours égale à 180 degrés, sont ancrés dans ces symétries. Nous les utiliserons aussi pour démontrer des propriétés moins connues, par exemple qu'il n'existe que 14 types différents de papiers peints.