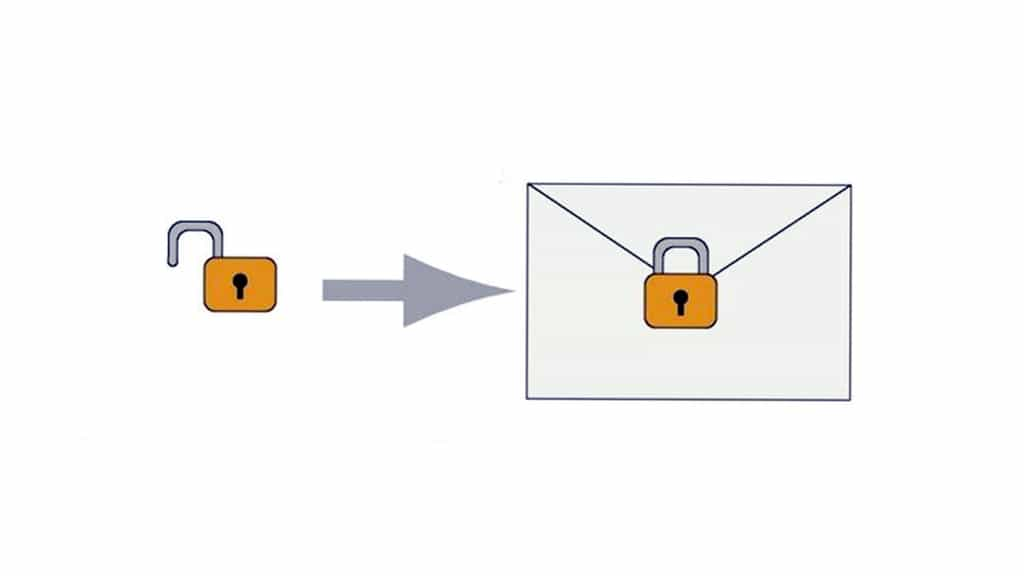
Notre besoin de communiquer de façon sécurisée se réalise aujourd'hui par ordinateurordinateur avec des personnes que nous n'avons jamais rencontrées, et que nous ne rencontrerons probablement jamais, qu'il s'agisse d'une commande sur un site de commerce électronique ou de la transmission d'une feuille de soins au centre de Sécurité sociale. Dans ce contexte, l'échange préalable d'une clé, opération obligatoire en cryptographiecryptographie traditionnelle, n'est pas envisageable.
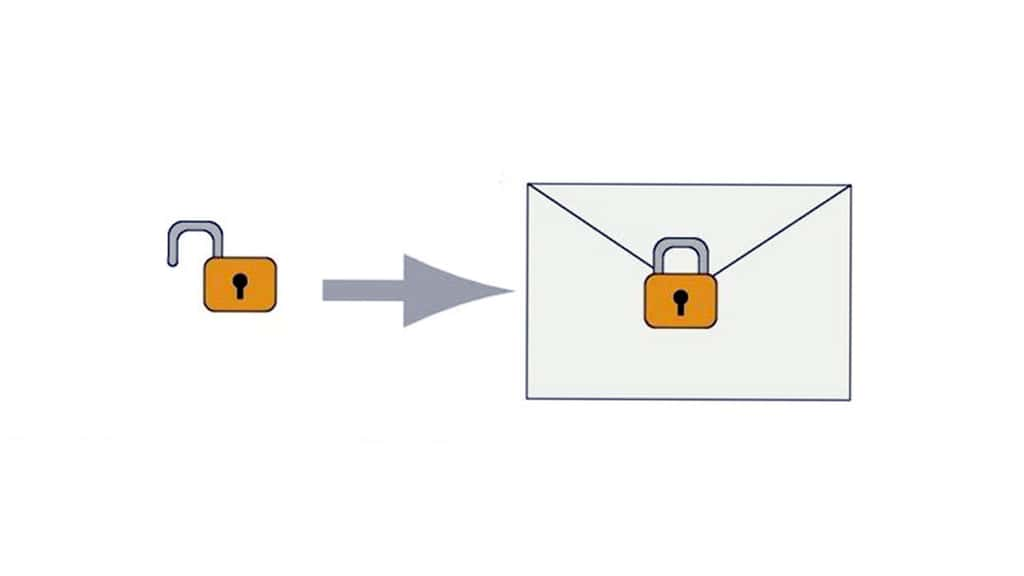
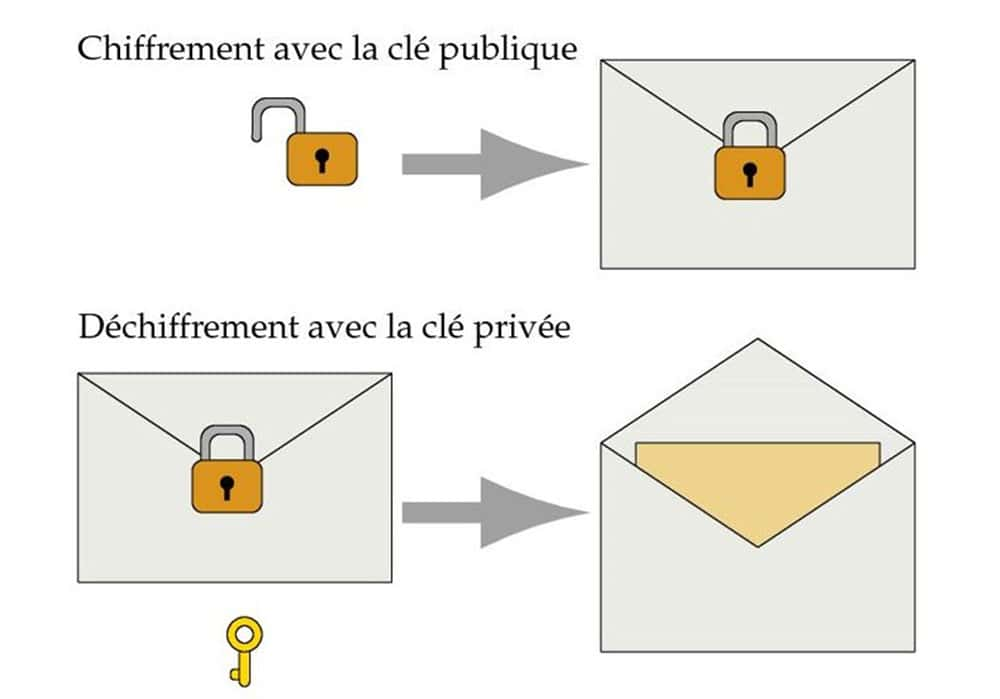
Dans le milieu des années 1970, l'invention de la cryptographie à clé publiqueclé publique, liée au développement des communications par ordinateur, a résolu le problème. Son principe repose sur une paire asymétrique de clés : l'une pour chiffrer, qui peut être publique, et l'autre pour déchiffrer, qui doit rester privée.
Pour communiquer secrètement avec un destinataire, je consulte dans un annuaire sa clé publique et je l'utilise pour chiffrer le message qui lui est adressé. Lorsqu'il recevra ce cryptogramme, il utilisera, pour le reconstituer en clair, sa propre clé de déchiffrementdéchiffrement qu'il garde secrète.
Le plus utilisé de ces mécanismes est le RSA, acronyme tiré du nom de ses trois inventeurs Ronald Rivest, Adi Shamir et Leonard Adleman qui l'ont publié en 1978.
La clé publique
La clé publique est constituée d'un module n public, égal au produit de deux facteurs premiers inconnus, et d'un exposant public e, souvent égal à 3. Ainsi, pour chiffrer un message m, codé comme un nombre compris entre 0 et n − 1, on l'élève à la puissance e modulo n. Si e vaut 3, cela revient à l'élever au cube modulo n. L'opération réciproque, à savoir l'extraction de la racine cubique modulo n est réputée être un problème difficile en l'absence de la connaissance de la factorisation de n.
La clé privéeclé privée est constituée des facteurs p et q de n. Grâce à la connaissance de ces facteurs, il est possible de déterminer un exposant privé d qui permettra de retrouver le message correspondant à un cryptogramme donné. L'exposant privé d est égal à l'inverse de l'exposant public e modulo le plus petit multiple commun à p − 1 et q − 1. La connaissance des facteurs p et q du module est requise pour ce calcul.
Le message est reconstitué en élevant le cryptogramme à la puissance exposant privé modulo n.
La fonction de chiffrementchiffrement RSARSA est ce qu'on appelle une fonction à sens unique avec trappe. Chacun peut chiffrer un message avec les paramètres publics. Toutefois, pour inverser le processus, c'est-à-dire pour retrouver le message à partir du cryptogramme, il faut disposer d'une information additionnelle : la trappe ou clé privée, maintenue secrète.

La sécurité de ce mécanisme repose de manière cruciale sur la difficulté de retrouver les facteurs p et q du produit n = p × q. Cela a relancé la recherche pour résoudre ce problème, comme le montre le tableau ci-dessus qui indique l'année où ont pu être factorisés les entiers de grande taille.