Le chiffrementchiffrement est resté longtemps confiné à des problèmes de traitement du langage écrit. Il s'agissait de remplacer une lettre par une autre, voire un mot par un autre. Il est aujourd'hui devenu majoritairement un calcul.

Le poète et cryptologue arabe Ibn Dunaynir
La première trace d'un procédé de chiffrement faisant explicitement appel à un calcul est due au poète et cryptologuecryptologue arabe Ibn Dunaynir (1187-1229) qui décrit ainsi son procédé : « Pour obscurcir un texte, on peut avoir recours au nombre correspondant à la lettre, puis de doubler une fois, ou deux fois, ou plusieurs fois, ce qui dissimulera le sens à la personne qui lit. Ainsi, on met "Ba", dont la valeur numérale est deux, à la place du "Alif", dont la valeur numérale est un. De même, on met "Sin", dont la valeur numérale est 60, à la place de "Lam", dont la valeur numérale est 30, et ainsi de suite pour tout le texte. Alors, admire cette jolie méthode ! »

Avant d'adopter la numération de position, les Arabes attribuaient une valeur numérale aux lettres de l'alphabet, de la même manière que les Romains attribuaient la valeur un à la lettre I, la valeur cinq à la lettre V, la valeur dix à la lettre X, etc. À la différence des Romains, les Arabes attribuaient une valeur numérale à toutes les lettres de leur alphabet. À titre d'exemple, en numération romaine, le mot « LIV » se coderait en CIIX après multiplication par deux et le mot « MIX » se coderait en DVL après multiplication par cinq.
Les connaissances mathématiques de son époque ne permettaient pas à Ibn Dunaynir de proposer des calculs beaucoup plus élaborés qu'un doublement ou un triplement des valeurs numérales. Le résultat d'opérations plus complexes serait vite devenu un nombre trop grand pour pouvoir être transcrit en lettres. Il en a été tout autrement après que Gauss eut introduit les congruences au début du XIXe siècle. Dans cette arithmétique, le résultat, lorsqu'il dépasse une certaine limite, est réduit par soustraction, ce que nous réalisons tout naturellement avec les horaires : cinq heures après 22 h font 3 h. Nous comptons les heures « modulo » 24.
Le codagecodage de chaque lettre de l'alphabet en un nombre entre 0 et 25 et la réduction du résultat dès qu'il dépasse la valeur 26 libèrent le concepteur et l'autorisent à imaginer des calculs aussi complexes qu'il le souhaite. Le résultat sera toujours un nombre compris entre 0 et 25 qui sera transcrit en une lettre dans le cryptogramme.
L'Américain Lester Hill
L'Américain Lester Hill a imaginé utiliser cette arithmétique pour concevoir en 1929 le premier système de chiffrement reposant sur un calcul algébrique. Son procédé repose sur le calcul matriciel. Chaque lettre de l'alphabet est codée de 0 à 25, comme on l'a vu, selon un codage tenu secret entre les correspondants, puis les lettres du message sont regroupées deux par deux. Les couples de lettres sont codés en nombres selon la convention pour obtenir un vecteur de dimension 2. Ce vecteur est multiplié par une matrice 2 × 2 pour obtenir un vecteur image qui correspondra au cryptogramme. Toutes les opérations sont réalisées modulo 26. Pour reconstituer le message en clair, il suffira d'effectuer l'opération inverse, en multipliant les vecteurs transcrits du cryptogramme par la matrice inverse de celle utilisée pour le chiffrement.
Il est possible de regrouper les lettres trois par trois et multiplier le vecteur résultat de dimension 3 par une matrice 3 x 3.
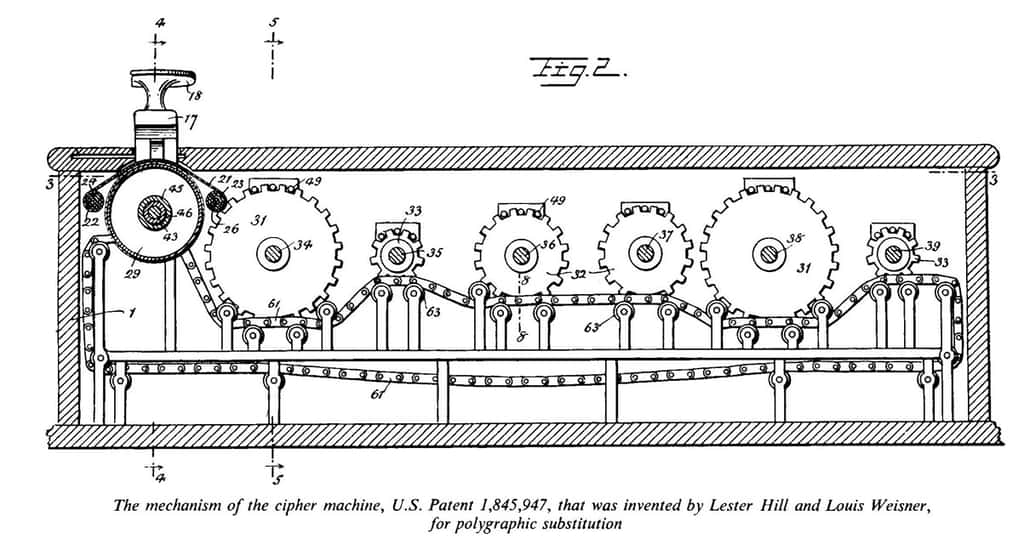
Le calcul à la main étant assez laborieux et sujet à de multiples erreurs, Lester Hill a inventé une machine, constituée d'une chaîne et de roues dentées, permettant de chiffrer jusqu'à des hexagrammes qui sont des groupements de six lettres. Ce chiffre a effectivement été utilisé par l'armée américaine pour crypter les indicatifs radio.