Cryptologie : les mondes d'Impagliazzo

Sans problème difficile, il ne peut pas y avoir de cryptologiecryptologie autre que celle du masque jetable. De plus, le titulaire de la clé doit pouvoir déchiffrer facilement le message, les problèmes de la cryptologie doivent donc être aisément vérifiables.

Ils doivent appartenir à la classe NP. Un problème appartenant à la classe NP sans appartenir à la classe P ne conviendrait pas forcément. On pourrait admettre l'existence d'un tel problème, qui serait difficile à résoudre dans le pire des cas, mais facile en général. Ce type de problème ne permettrait pas de réaliser une cryptologie applicable. Le cryptogramme doit être indéchiffrable quel que soit le message, et non dans le pire des cas seulement.

Le chercheur américain Russell Impagliazzo a imaginé des mondes (listés dans le texte et empilés sur la pyramide de la figure suivante) selon les résultats futurs que la théorie de la complexité nous apportera. © Bohmmartin, wikimedia commons, CC 4.0

Cryptomania

Cryptomania est le monde dans lequel nous vivons virtuellement. Il existe des fonctions à sens unique avec trappe. On peut poser un problème difficile et donner une indication à certains seulement pour qu'ils puissent le résoudre. Le problème restera difficile pour les autres. C'est ce qui se passe avec la fonction RSA : le déchiffrementdéchiffrement est impossible, sauf pour ceux qui connaissent la factorisation du module.

Minicrypt

Ce monde imaginaire pourrait devenir réel si on pouvait démontrer que toute fonction à sens unique ne peut pas avoir de trappe. Cela remettrait en question le chiffrementchiffrement à clé publique, mais on pourrait toujours signer les documents. La réalisation d'une fonction de signature se contente de l'existence d'une fonction à sens unique. Dans ce monde, un professeur peut poser un problème difficile à sa classe, mais ne peut pas donner d'indication à certains seulement pour le résoudre.

Pessiland

Selon Impagliazzo, ce monde imaginaire serait le pire qui soit. Il y existe des problèmes faciles à vérifier, mais difficiles à résoudre, et pas de fonction à sens unique. Toutes les fonctions facilement calculables y sont aussi facilement inversibles. Certains problèmes restent difficiles, mais cette difficulté ne se traduit par aucun avantage pour réaliser de la cryptographiecryptographie. Dans ce monde et dans les suivants, aucune cryptologie autre que le masque jetable n'est envisageable.

Heuristica

Dans ce monde, les problèmes faciles à vérifier sont en moyenne aussi faciles à résoudre, mais il peut rester des instances difficiles. Cela commence à être satisfaisant pour les applications. Par exemple, dans la plupart des cas, le marchand de pommes pourra facilement choisir les fruits de son étalage afin de satisfaire un client qui lui en demande pour un certain poids.

Algorithmica

Ce monde est finalement celui où P = NP. Tout problème facile à vérifier est facile à résoudre, y compris dans le pire des cas.

Les cinq mondes d'Impagliazzo. Ce sont des mondes imaginaires envisageables en l'état actuel de nos connaissances. Le développement de la théorie pourrait soit les rendre réels, soit les faire disparaître. Toute la cryptographie, et en particulier le chiffrement à clé publique, appartient à Cryptomania qui est notre monde empirique actuel. Le chiffrement symétrique et la signature à clé publique appartiennent au monde Minicrypt. La seule cryptographie utilisable dans les autres mondes est la cryptographie inconditionnellement sûre, comme le chiffre de Vernam avec bande aléatoire. Il est étonnant de constater que la signature à clé publique appartient au monde Minicrypt, alors que le chiffrement à clé publique appartient, lui, au monde Cryptomania. © P. Guillot

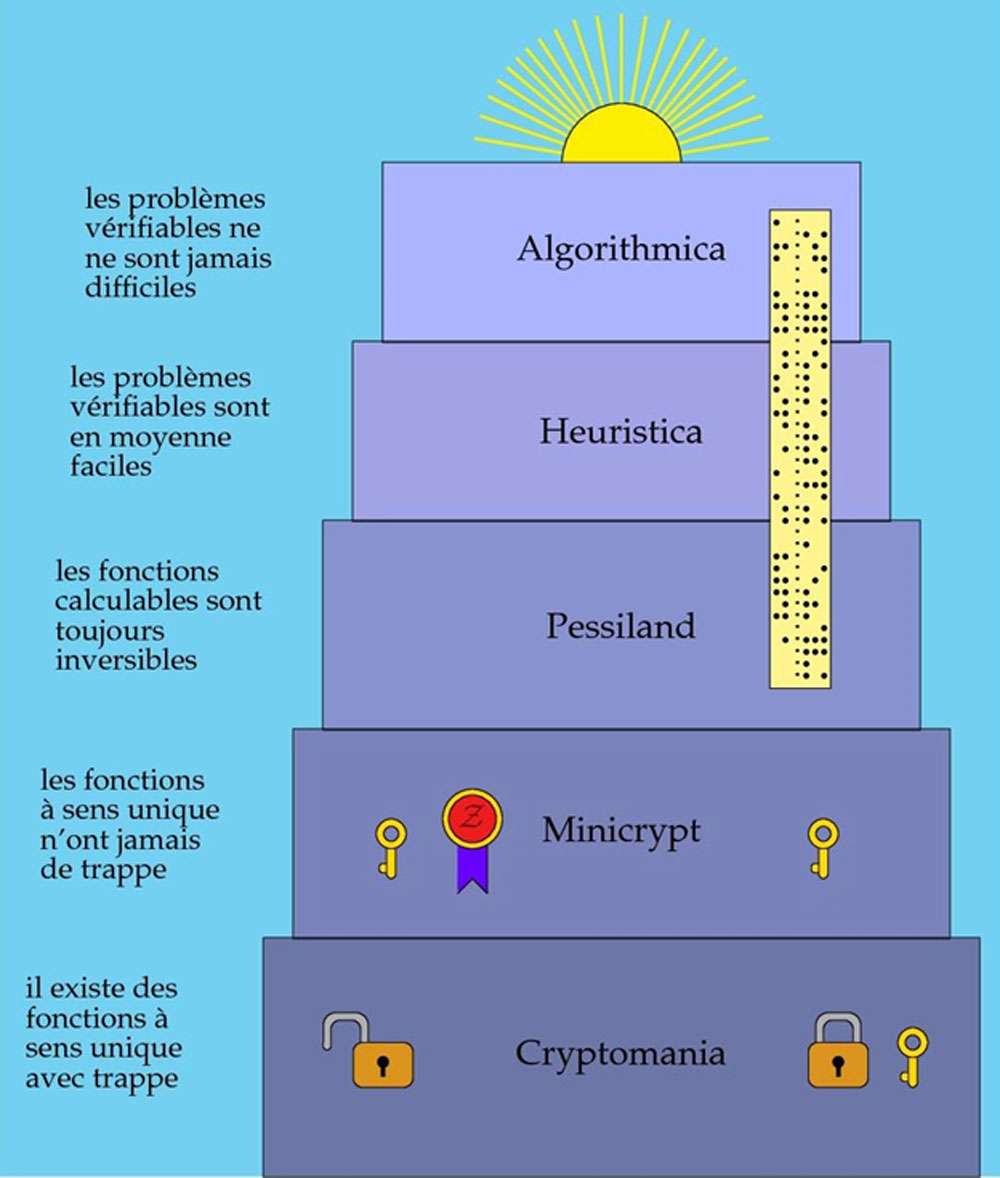
Ces mondes constituent une hiérarchie de mondes possibles ou impossibles selon que la théorie de la complexité démontrera l'existence de problèmes difficiles ou l'infirmera en découvrant des algorithmes efficaces pour les résoudre.