La cryptographiecryptographie contemporaine s'appuie sur des fonctions à sens unique. Ces fonctions sont facilement calculables, mais il est pratiquement impossible, avec une valeur, de retrouver le paramètre qui a conduit à cette valeur. Par exemple, en choisissant deux grands nombres premiers, il est facile de les multiplier. Actuellement, le seul produit ne permet pourtant pas de retrouver les facteurs si ceux-ci sont choisis assez grands. La multiplication des entiers est une fonction à sens unique. Elle est un cas particulier des problèmes qu'on ne sait pas résoudre, mais, une fois la solution connue, il est aisé de la vérifier.
Si je vous donne, par exemple, le défi de factoriser le nombre 2.027.651.281, vous aurez sans doute beaucoup de mal à trouver les facteurs sans un outil performant de calcul. En revanche, si je vous annonce que ces facteurs sont 46.061 et 44.021, une minute vous suffira pour vérifier que cette solution est la bonne.

Le souci est que l'existence de tels problèmes n'est pas assurée. Les chercheurs n'ont pas pu jusqu'à présent prouver que la factorisation des entiers était vraiment un problème difficile. La seule observation que nous puissions faire est que, dans l'état actuel de nos connaissances, ce problème est loin d'être aisé à résoudre. De nombreux et impressionnants progrès ont été accomplis depuis que les mathématiciens s'y intéressent. La résolutionrésolution est passée en quelques dizaines d'années d'une complexité exponentielle à une complexité sous-exponentielle en fonction du nombre de chiffres du nombre à factoriser. Les progrès s'arrêteront-ils là, ou d'autres progrès sont-ils encore à espérer ?
La machine de Turing
On ne sait toujours pas si c'est seulement notre ignorance d'algorithmes plus performants qui rend la factorisation difficile, ou si cette difficulté est dans la nature même du problème. Les notions de calculabilité et de complexité du calcul ont été modélisées par Alan Turing dans une machine abstraite. La machine de Turing comprend :
- une unité centrale de calcul qui peut se trouver dans un nombre fini d'états ;
- un ruban illimité où figurent au départ les données à traiter, et où s'écrivent les résultats ; ces données s'expriment à l'aide d'un alphabet de taille finie ;
- une tête de lecture-écriture qui peut remplacer un caractère par un autre sur le ruban, ou bien déplacer le ruban d'une position vers la gauche ou vers la droite.
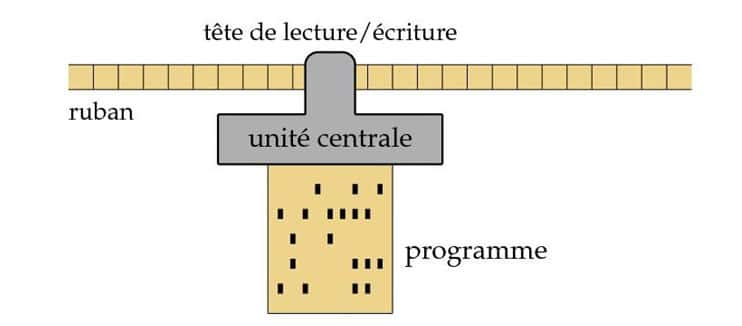
Le programme d'une telle machine est une liste d'instructions constituées chacune de quatre données : un état q, un symbole s, un nouvel état r, et une action a de la tête de lecture. Si la machine se trouve dans l'état q, et si elle lit le symbole s sur le ruban, alors elle passe dans l'état r et réalise l'action a qui consiste soit à écrire un symbole sur le ruban à la place de s, soit à déplacer le ruban dans un sens ou dans l'autre.
Une machine de Turing est dite « déterministe » si son programme ne comprend qu'une instruction pour un état et un symbole donnés. Un problème appartient à la classe P (pour « polynomial ») s'il existe une machine de Turing déterministe qui le résout en exécutant un nombre d'instructions borné par un polynôme de la taille des données. Un problème n'appartenant pas à cette classe sera tenu pour difficile, du moins pour certaines données.
Si, au contraire, il existe plusieurs instructions possibles correspondant à un état et un symbole donnés, la machine est dite « non déterministe ». Une machine non déterministe résout le problème s'il existe une suite d'instructions qui conduit au résultat, autrement dit s'il existe un oracleoracle qui indique à la machine quelle est la bonne instruction à exécuter parmi plusieurs choix possibles. On peut simuler une machine non déterministe avec un nombre illimité de machines déterministes, chacune choisissant l'une des instructions à exécuter dans un état donné. Un problème appartient à la classe NP s'il existe une machine de Turing non déterministe qui le résout en un nombre d'instructions borné par un polynôme de la taille des données. Ce sont précisément les problèmes qui se vérifient aisément, la solution jouant le rôle d'oracle qui indique le choix des instructions conduisant au résultat.
Si un problème appartient à la classe P, alors il appartient aussi à la classe NP. Un des grands problèmes ouverts de la théorie de la complexité est de savoir si la classe NP est strictement plus grande que la classe P ou non, question qui peut se résumer ainsi : existe-t-il un problème aisément vérifiable qui est difficile à résoudre ?
Si un tel problème existe, ce qui n'est toujours pas prouvé, la factorisation des entiers est un candidat vraisemblable.