Hasard et chaos : la théorie des systèmes dynamiques

Que le hasard existe vraiment dans le monde ou pas, nous ne pouvons pas le savoir. Il y a une raison profonde à cela : un tas de phénomènes nous paraissent aléatoires, mais on finit par y découvrir des lois. Si ces lois sont complexes et font intervenir de nombreuses variables, comme en météorologiemétéorologie, il est très difficile d'en prédire les effets à long terme.

La météorologie fait partie de ces domaines où, malgré une connaissance correcte des lois en jeux, nous ne savons prédire qu’à court terme. © NG

Pour la météorologie, on comprend bien que tous les possibles désagréments s'accumulent pour prendre les vacanciers au dépourvu :

• Les lois ne sont pas parfaitement connues ;
• De nombreuses variables interviennent (composition de l'air, températures, pression, effets du soleil, effets de l'homme, des animaux...) ;
• Comme si ça ne suffisait pas, il est impossible de connaître précisément ces variables. Par exemple, on peut mesurer la température en certains points de l'atmosphèreatmosphère, mais pas partout évidemment. Sans compter que la précision de la mesure n'est jamais parfaite.

Tout cela contribue à faire qu'il est matériellement impossible de prédire le temps qu'il fera dans une semaine. Que faudrait-il donc faire pour permettre de magnifiques prévisions et justifier le salaire des présentateurs de la météo télévisée ? Connaître parfaitement les lois ? Se ramener à très peu de variables ? Les mesurer de manière plus précise ?

Imaginons toutes ces merveilles réunies. Nous connaissons parfaitement les lois qui gèrent l'évolution d'une variable, nous connaissons avec une grande précision les valeurs de cette variable au départ, et nous voulons prévoir l'évolution de la variable. Cela semble assez simple... Mais ne l'est pas.

La théorie des systèmes dynamiques

C'est ce que prouve, en mathématiques, la théorie des systèmes dynamiques, dont le chaos est un objet d'étude.

Prenons l'exemple d'une fonction donnée par f(x) = 4x(1-x), et supposons qu'une grandeur x évolue en suivant la fonction f. Par exemple, à un certain instant, la grandeur est x₀. Une seconde après, elle vaut f(x₀)=x1, et ainsi de suite. Cela nous permet de définir une suite x₀,...,xn,... dont nous pouvons facilement calculer les valeurs exactes si l'on connaît x₀. Pour autant, nos ennuis ne sont pas tout à fait terminés, parce ce que dans le monde réel, la « mesure » qui donne x₀ n'est jamais parfaite, et il faut admettre qu'on fera sans doute une petite erreur...

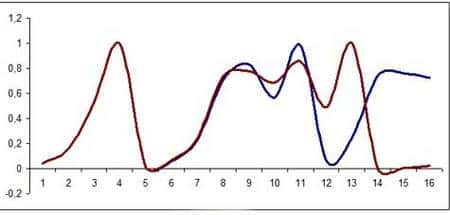
La suite récurrente définie par f(x) = 4x(1-x), pour deux valeurs très proches de x₀ (0,0411 en marron, et 0,0412 en bleu). Bien qu’on ne distingue pas les courbes, très proches, jusqu’à la huitième étape, elles s’écartent ensuite rapidement, illustrant l’effet dramatique d’une petite erreur initiale.

Propriétés d'un système chaotique

Or, la prise en compte cette cette petite incertitude débouche sur trois propriétés déroutantes de notre « système dynamique » (c'est-à-dire la suite des xn) :

1. La moindre erreur augmente jusqu'à devenir ingérable : c'est la dépendance aux conditions initiales.
2. L'allure même de la suite (croissante, décroissante, etc.) dépend de la moindre petite erreur : c'est la densité des points périodiques.
3. L'augmentation de l'erreur est telle que, dès que n est un peu grand, nous ne pouvons plus rien dire sur la valeur de xn : c'est la propriété de mélange.

La manière dont le lait se mélange au café est chaotique. © NG

Ces trois propriétés définissent ce qu'on appelle un système chaotique. Ce que montrent les systèmes chaotiques c'est qu'une incertitude minime peut irrémédiablement conduire à une totale impossibilité des prévisions. Cela a souvent été interprété comme un exemple de hasard, dans le sens où le comportement du système est imprévisible, donc (c'est une définition du hasard), aléatoire.

Mais si l'on est plus rigoureux, on comprend que ce « hasard » n'existe que parce qu'il y a déjà, au départ, un petit hasard, une petite incertitude sur la condition initiale. Un système chaotique n'est donc pas « une machine à fabriquer du hasard », mais « une machine à amplifier du hasard ».

Des chercheurs en sciences cognitivessciences cognitives tentent depuis des décennies (sans grand succès pratique pour l'instant) de formaliser l'idée que le cerveaucerveau humain est chaotique, ce qui rendrait l'Homme en partie imprévisible pour les observateurs... et pourrait nous donner l'illusion du libre arbitre.