Le hasard existe-t-il ?

Le hasard existe-t-il ? Chez l'Homme, difficile en tout cas de véritablement « choisir au hasard ». La preuve avec cette expérience.

La salle était remplie de 45 étudiants mous de psychologie, peu intéressés par la statistique et ses arcanes. Ma mission, si je l'acceptais, était de leur faire comprendre, ce jour-là, comment on peut déterminer si des réponses proviennent ou non d'un hasard équiprobable. Honte sur moi : je n'avais pas préparé assez d'exercices, et me voilà pris au dépourvu, avec une demi-heure à combler et rien à leur mettre sous la dent, qu'ils ont souvent dure. Il fallait improviser.

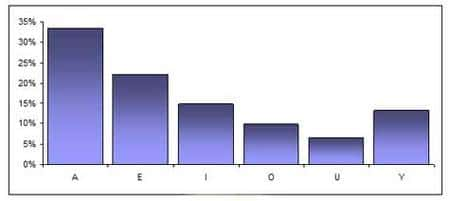
Je demandais à chaque étudiant d'inscrire sur un bout de papier une voyelle (A, E, I, O, U ou Y) « au hasard », en faisant en sorte de choisir la lettre comme si on l'avait tirée par une méthode aléatoire équiprobable (c'est-à-dire sans privilégier une lettre par rapport à une autre). On relève les réponses, qui nous permettent de dessiner une forme de graphique qu'on retrouvera systématiquement dans les réplicationsréplications.

Pourcentage de personnes donnant chaque voyelle « au hasard ».

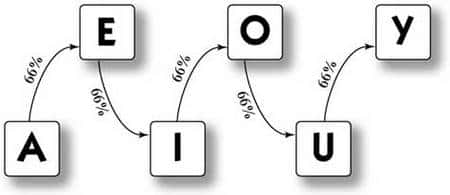
On peut comprendre la forme de la distribution des voyelles en imaginant une marche aléatoire le long d’un chemin à sens unique reliant les voyelles dans l’ordre. À chaque étape, on s’arrête avec une probabilité de 33 %, sauf si l’on est arrivé à « Y », auquel cas la marche est terminée.

Comment percevons-nous le hasard ?

La conclusion qui découle de ces données, c'est que nos efforts pour être aléatoires ne sont que partiellement couronnés de succès.

Et voilà comment un accidentaccident de planification m'amena à m'intéresser à la manière dont nous percevons le hasard... et à faire le lien avec ce que nous en disent les mathématiques.

Lorsqu'on parle de hasard et de mathématiques, tout le monde pense aussitôt aux probabilités. Pourtant, d'autres domaines des mathématiques ont leur mot à dire, et souvent de manière bien plus fondamentale, que les probabilités. Si les probabilités sont d'une utilité indiscutable pour mesurer le hasard, elles n'en fournissent pas (ou indirectement) de définition.