Le nombre d'or et la beauté des spirales en botanique

La suite de Fibonacci et le nombre d'or favorisent les spirales de la botaniquebotanique plutôt qu'un penchant esthétique des plantes. On ne peut s'empêcher de constater que c'est l'arrangement spiralé correspondant à la divergence d'or qui flatte l'œilœil par sa compacité et son harmonie.

On s'est efforcé de convaincre le lecteur que les spirales en botanique ne sacrifient pas à un penchant esthétique des plantes ou des abeilles lorsqu'elles favorisent la suite de Fibonacci et le nombre d'or.

La coquille du nautile dessine une spirale logarithmique. © Domaine public

Le nombre d'or en botanique

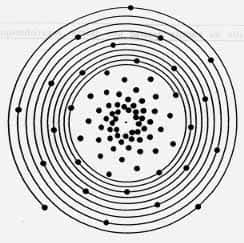
Il vaut la peine de montrer à ce même lecteur à quel point le nombre d'or, malgré tout, mérite en botanique la réputation que lui ont faite Phidias et ses successeurs. La figure, ci-dessus, représente une série de points qui reproduisent fidèlement les arrangements que l'on trouve dans la marguerite ou le tournesoltournesol. Chaque point appartient à deux spirales bien visibles orientées respectivement à gauche et à droite.

Pour construire ces réseaux spiralés, il suffit d'aligner ces points sur une spirale logarithmique unique de sorte que chaque point soit séparé du précédent par un angle fixe que les botanistesbotanistes nomment la divergence. Le nautile forme la spirale en appliquant une règle très simple : il habite la dernière chambre de sa coquille tant qu'il y est à l'aise. Or il ne cesse de grandir, il doit un jour quitter sa cellule au profit d'une chambre plus grande qu'il fabrique sur le modèle de la précédente. Ce qui confère à la coquille ses caractéristiques et lui donne droit à l'adjectif « logarithmique », c'est que deux chambres consécutives forment toujours le même angle entre elles alors leurs tailles sont également dans un rapport fixe.

L'angle d'or dans les spirales des plantes

Un angle peut se mesurer en degrés si l'on divise ce nombre par 360° (un tour complet), on fait appel à une autre manière de désigner les angles. C'est ainsi qu'un quart de tour ou un demi-tour correspondent à des angles de 90° ou 180° : la différence est purement verbale. On retrouve l'angle d'or dans la nature : ananasananas, palmier, tournesol... La plante respecte un angle de rotation constant lors de sa croissance qui tend vers le nombre d'or. Cet angle d'or permet d'optimiser au maximum d'espace.

En foi de quoi, il arrive que l'on parle de divergence d'or. C'est un angle qui vaut 222°, 492°... Il correspond à un déplacement angulaire égal à 360° multipliés par le nombre d'or et vaut 582°, 492°... Comme cet angle dépasse 360°, il est équivalent à 582°, 492°... -360° (un tour complet n'a d'autre effet que de ramener un point à sa position initiale.)

La spirale « génératrice » représentée par le trait continu porte une série de points qui imitent les arrangements botaniques. Deux points successifs le long de la spirale sont séparés par une distance angulaire constante.

Les arrangements et l'esthétique : un hasard ?

Lorsqu'un arrangement spiralé fait appel à la suite de Fibonacci comme on l'a présenté en introduction, c'est que la divergence est très proche de la divergence d'or. Mais il y a plus, la divergence d'or correspond à l'arrangement le plus esthétique (bien sûr, cette affirmation n'a pas de signification en mathématique. Ce qui ne veut pas dire qu'elle soit absurde). Les réseaux spiralés représentés ici ont été construits sur la même spirale logarithmique. Seul diffère dans chacun des cas la valeur de la divergence, et les écarts sont faibles (ils ne dépassent pas un demi-degré d'une valeur de la divergence à la valeur voisine). Les aspects des réseaux, en revanche, varient beaucoup. On ne peut s'empêcher de constater que c'est l'arrangement spiralé correspondant à la divergence d'or qui flatte l'œil par sa compacité et son harmonie. De fait, et même si ce n'est pas visible au premier coup d'œil, le nombre d'or attribue au réseau associé une symétrie plus grande, la « symétrie d'échelle » qui se manifeste ici dans le domaine de la géométrie de la plante.