au sommaire
La suite de Fibonacci est une suite d'entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent. Elle doit son nom à Leonardo FibonacciLeonardo Fibonacci, un mathématicienmathématicien italien. Le nombre d'or, lui, semble être très présent dans la nature sous des formes multiples, dans les végétaux : phyllotaxie (disposition des feuilles), géométrie des fleurs... mais aussi en architecture et dans les arts.
Le plus grand titre de gloire de Leonardo Fibonacci, ou Leonardo de Pisa, est d'avoir popularisé en Occident la numérotation indo-arabe appelée à supplanter progressivement la numérotation romaine si peu adaptée aux opérations arithmétiques les plus simples. Si vous en doutez, essayez de multiplier IX par XLVIII !
La suite de Fibonacci : une suite infinie
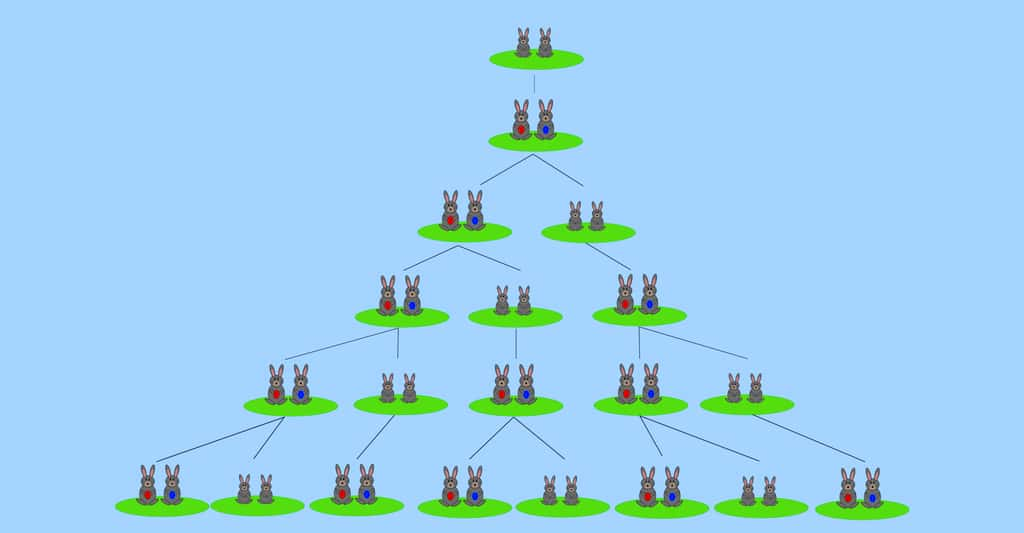
Mais Leonardo Fibonacci est aussi connu pour avoir mis en évidence la série qui porteporte désormais son nom. Il n'est pas nécessaire de mémoriser chacun des termes de la suite (elle est infinie). Il suffit de se rappeler sa règle de constructionconstruction : à l'exception des deux premiers, chaque terme de la suite est égal à la somme des deux termes qui le précèdent immédiatement. Par exemple : 21 = 8 + l3 ; 55 = 21 + 34.

La suite de Fibonacci a une série impressionnante de propriétés qui font la joie des amateurs de mathématiques amusantes. Nous n'en retiendrons qu'une, car elle est importante pour ce qui va suivre : le rapport de deux nombres consécutifs de la suite est alternativement supérieur et inférieur au nombre d'or qui vaut exactement (1+√5)/2 = 1.61803398...
En effet : 13/8 = 1.625 ; 21/13 = 1.61538... ; 34/21 = 1.61904... et ainsi de suite. Plus on avance dans la suite de Fibonacci et plus l'écart s'amenuise.
Pour un mathématicien ou physicienphysicien, c'est un nombre remarquable en ce sens qu'on le voit surgir dans des domaines apparemment très éloignés de la suite de Fibonacci. On peut citer le pentagone régulier ou la théorie du chaos.

Le nombre d'or dans l'art et l'architecture
Le nombre d'or déborde largement les mathématiques. Les anciens Grecs le connaissaient. Ce n'est pas une coïncidence, semble-t-il, si le fronton du Panthéon est inscrit dans un rectangle dont les longueurs des côtés adjacents ont le nombre d'or comme rapport ; si ce même rapport apparaît fréquemment dans les statues de Phidias. Les peintres ou architectesarchitectes « modernes » comme Botticelli, Dürer, Dalí ou Le Corbusier, pour ne citer qu'eux, ont suivi l'exemple des anciens. Dans certains cas, il est possible que l'on ait voulu voir dans une œuvre ce que leur créateur n'y avait jamais mis. Ce ne serait pas la première fois que les critiques auraient outrepassé leurs compétences.
Il n'en reste pas moins que le nombre d'or, dans notre civilisation, a été associé à des qualités esthétiques particulières. L'influence pythagoricienne n'est sans doute pas absente de cette identification dont l'histoire a prouvé la solidité. Mais quelle relation peut-il y avoir entre le nombre d'or et les plantes ?