La masse des particules

Comment expliquer que certaines particules soient massives et que d'autres comme le photon n'aient pas de masse de repos ? La question est complexe et requiert une analyse détaillée dans le dossier consacré à la physique quantique. Cette question est en effet du ressort des physiciensphysiciens des particules élémentaires. La description des interactions s'explique au moyen de champs vectoriels mais les bosons vecteurs de ces interactions n'ont à l'origine pas de masse et leur portée est infinie. Si cela s'applique très bien au photon, vecteur de l'interaction électromagnétique, ce modèle ne s'applique pas aux 12 autres bosons connus (auxquels il faut ajouter 12 bosons X ety Y de masse supérieure à 10¹⁵ GeVGeV dont la charge électrique est fractionnaire).

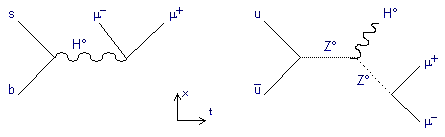
Rappelons tout d'abord que les interactions permettent de décrire la création de particules lors de collisions à hautes énergiesénergies. Ces lois conservent les énergies de la réaction. Le boson Z° par exemple peut se transformer indifféremment en quarksquarks et leptonsleptons, les deux familles de particules élémentaires qui forment la matièrematière, chacune apparaissant par paire avec son antiparticuleantiparticule (quark uquark u et antiquark u, électronélectron et positronpositron, etc). La création du boson Z° massif est donc une condition initiale sine qua non de la formation de notre universunivers.

Ainsi que l'avaient prédit Yang et Mills, les équationséquations prédisaient que les bosons W et Z° de l'interaction faibleinteraction faible étaient très lourds. Comme l'on dit en physique quantique, ils n'obéissaient pas aux lois de symétrie. Comment pouvait-on les alourdir ? Les physiciens comprenaient bien que les gluonsgluons ne pouvaient pas d'eux-mêmes provoquer une brisure de symétrie et acquérir leur masse. Il fallait donc amender la théorie des particules élémentaires et tenir compte d'un second mécanisme que les cosmologistes ont vite récupéré. L'idée était qu'un boson vecteur interagissait avec le champ scalaire et de spinspin égal à 0 qui se caractérisait par une seule quantité : le nombre d'état de spin.

Cette explication devait surmonter plusieurs difficultés. Le fait que la symétrie se brisa spontanément devait logiquement impliquer que l'énergie du vide quantique n'était pas nulle. Si c'était le cas, aucun processus quantique ne pourrait en "émerger". En d'autres termes, le vide quantique devait potentiellement avoir une énergie colossale. Un autre problème était qu'en partant d''une invariance de jauge globale, les modèles mathématiques prédisaient que la théorie électrofaiblethéorie électrofaible devait prévoir au moins un boson intermédiaire sans masse, Z°. Or l'interaction faible n'a qu'une portée finie. Autre contrepoint, par définition un seul état d'énergie minimale ne permet pas de briser une symétrie. Heureusement cette particule est capable de provoquer un spectrespectre d'états d'énergie minima. Mais le gros défaut de cette théorie est la portée infinie du boson de Goldstone, Z°.

Le mécanisme de Higgs Le mécanisme de Higgs rend massif des bosons vecteurs de masse nulle au repos, tel le photon, rendant ainsi la théorie plus cohérente. L'état de spin transverse (dans le sens du mouvementmouvement) qui n'existe pas pour le photon serait ainsi "mis en lumièrelumière". Son origine se trouve dans une interaction avec le champ scalaire du boson de Higgsboson de Higgs sans masse. Cette théorie est utlisée dans le modèle inflationnaire d'Alan Guth. Les physiciens se sont alors reportés sur une symétrie de jauge locale. Comme par enchantement, le boson de Goldstone se voit "absorbé" par un boson de Yang-MillsYang-Mills et celui-ci acquiert une masse, ce qui limite son influence à l'échelle atomique. Forts enthousiastes, les physiciens tenaient là un début de solution. Cette théorie était séduisante mais loin d'être parfaite. Il restait d'autres difficultés. La théorie de l'EDQ n'était renormalisable qu'à la condition que la masse du photon soit nulle. Or les bosons massifs vecteurs de l'interaction faible rendaient impossible toute renormalisation. Le modèle proposé par Glashow, Salam et Weinberg devait donc en tenir compte, ne fut-ce que dans un mécanisme secondaire qui briserait la symétrie entre l'électromagnétismeélectromagnétisme et l'interaction faible. Enfin, les théories de symétrie calculaient avec des champs scalaires, des valeurs pures, bref des particules sans masses (le modèle de Bludman), ce qui n'était pas conforme à la réalité. Le mécanisme secondaire invoqué était une symétrie interne de la dynamique quantique électrofaible (de saveur) dans laquelle agissait une nouvelle force capable de créer des particules de masse non nulles, les bosons, sans introduire de termes infinis, c'est-à-dire tout en étant renormalisable. Boson vecteur sans masse + Boson scalaire sans masse = Boson vecteur massif La création des particules de Higgs A gauche la transformation d'un quark bottom (b) en quark étrangequark étrange (s) avec production d'une paire de muonsmuons m-m+. Cette décroissance requiert un courant neutrecourant neutre véhiculé par une hypothétique particule de Higgs, H°. A droite l'annihilation d'une paire de quarks u-anti u avec production d'un boson Z° qui produit un boson de Higgs H° tandis que l'énergie restante crée une paire de muonsm-m+.Document