au sommaire
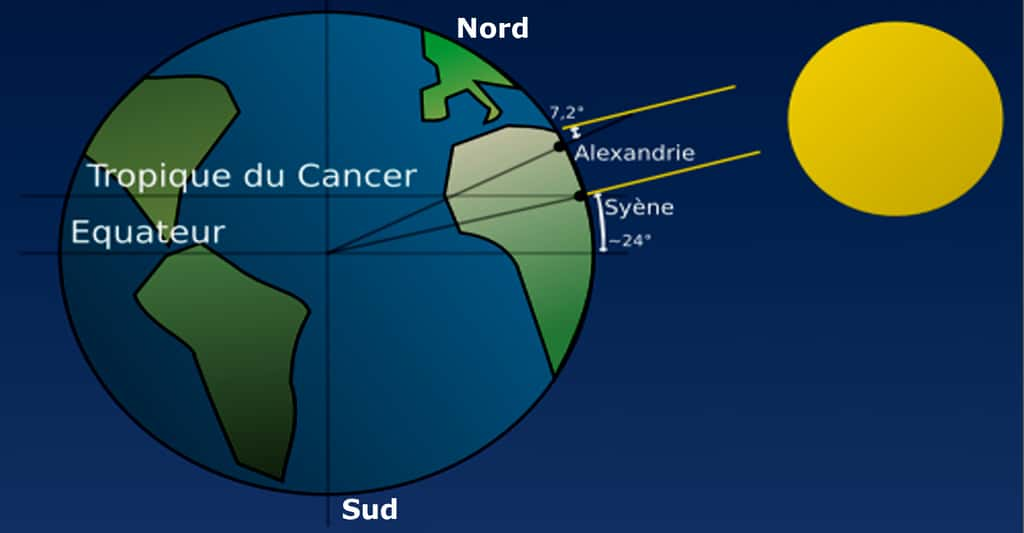
Curieusement, la détermination de la distance Syène-Alexandrie est aussi objet de polémiques. C'est d'autant plus étonnant que ces deux localités du bord du Nil étaient reliées par un trafic important de marchandises : les marges de ce fleuve nourricier de l'Égypte étaient divisées en parcelles agricoles.
ÉRATOSTHÈNEÉRATOSTHÈNE, conservateur de la bibliothèque d'Alexandrie, avait presque certainement à sa disposition des cartes ou des cadastrescadastres où devaient figurer les relais de halage. Les positions de ces relais « étaient connues avec précision », affirme Jacques BLAMONT, qui continue ainsi : « les haleurs utilisaient comme unité de longueur le schène, nom de la corde qui servait à tirer les bateaux. PLINE, poursuit-il, nous dit comment ÉRATOSTHÈNE convertissait les schènes en stades » (cf. bibliographie, p. 100). Cependant, DELAMBRE qui évoque cette unité parle de « schènes de différentes longueurs, en sorte que, d'une province à l'autre, un même nombre de schènes indiquait des distances assez différentes ». Ainsi, notre problème de la connaissance de la distance Syène-Alexandrie reste entier.
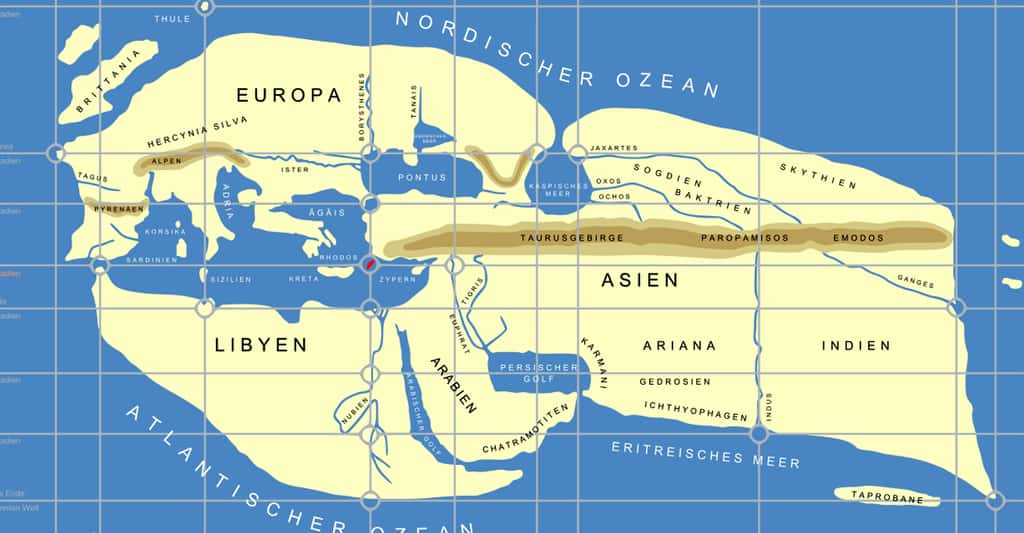
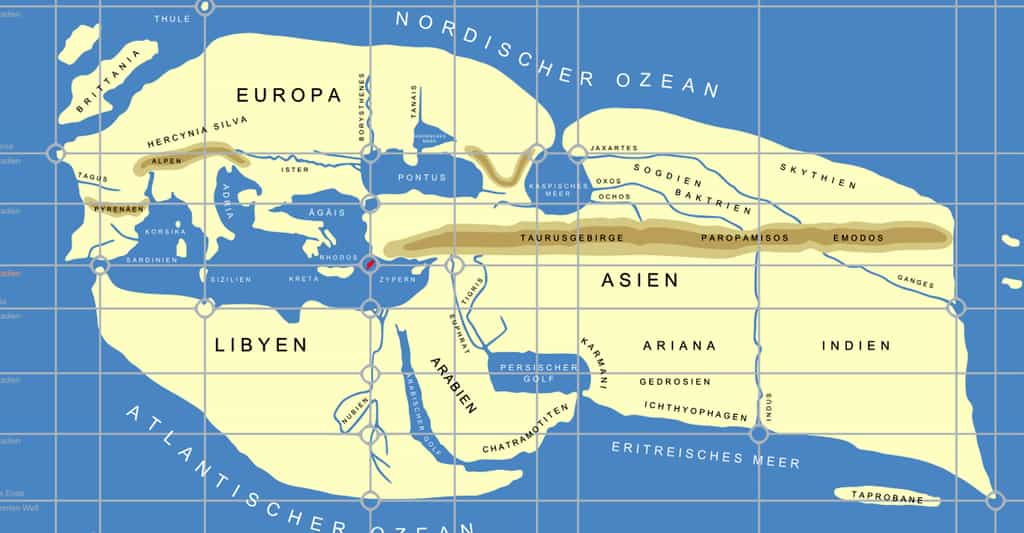
La reconstruction au 19ème siècle de la carte d'Ératosthène du monde connu. © Magenta Green - CC BY-SA 3.0
Il est vrai que depuis longtemps ALEXANDRE et les PtoléméesPtolémées avaient fait arpenter les chemins d'Égypte : les distances s'évaluaient alors en temps de marche ou en pas. D'ailleurs, la profession de « compteurs de pas » a laissé deux noms célèbres, DIOGNÈTE et BÉTONBÉTON. HÉRODOTEHÉRODOTE donne même la recette qui transforme une durée de marche en distance : un voyageur solitaire avance en une journée de 200 stades, alors qu'une troupe ne progresse que de 150.
Les 5 000 stades utilisés par ÉRATOSTHÈNE entre Syène et Alexandrie résulteraient donc de ces initiatives et de quelques corrections ajoutées par le savant pour tenir compte des ondulations de la route. À la fin des calculs, il introduit une dernière modification : après avoir divisé 250 000 par 360, il trouve 694,44 stades par degré de méridien, résultat qu'il rejette. Il l'arrondit à 700 pour avoir un nombre entier de stades par degré, ce qui le conduit donc à attribuer 252 000 stades pour la circonférence terrestre.