au sommaire
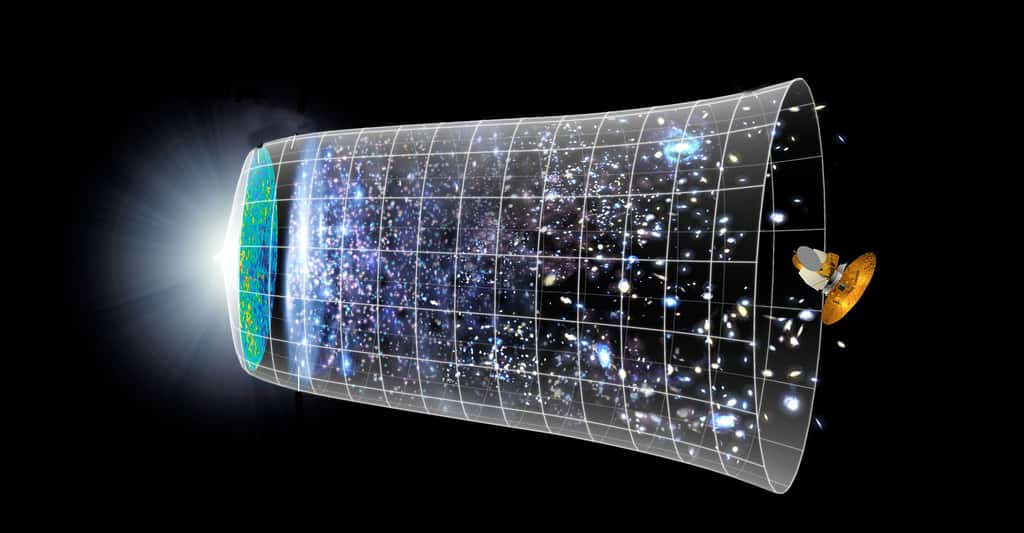
La révolution cosmologique du début du XXe siècle est le fruit de la conjonction entre l'avancée théorique fournie par la relativité générale d'EinsteinEinstein et les progrès observationnels. Découvrez les notions d'univers relativiste et d'espace-temps.

La relativité générale bouleverse les concepts même de temps et d'espace. L'univers n'est plus une structure d'espace (euclidien) immuable, dans laquelle se déroulent des phénomènes mus par des forces ; il devient un espace-temps « déformable », ce que les mathématiciensmathématiciens nomment « une variété à quatre dimensions » (trois pour l'espace, une pour le temps), déformée par la présence de matière.
La gravitation, une manifestation de la courbure de l'espace-temps
Cette déformation correspond à la gravitationgravitation, qui devient une manifestation de la courbure de l'espace-temps. À ce titre, elle dicte les trajectoires possibles des particules matérielles et des rayons lumineux, astreints à épouser les contours de la géométrie courbe.

Les équationséquations fondamentales de la relativité (les équations d'Einstein) décrivent la manière dont le contenu matériel de l'univers détermine la géométrie de l'espace-temps. La théorie permet ainsi une description de l'univers dans son ensemble, selon des modèles cosmologiques plausibles.
Bien entendu, parmi l'ensemble de solutions que permet la théorie, certaines seulement décrivent correctement notre univers en accord avec les observations astronomiques. En tout état de cause, le caractère non euclidien de l'univers apparaît dès lors non plus comme une étrangeté, mais au contraire comme une nécessité physiquephysique pour rendre compte des phénomènes gravitationnels : la courbure est reliée à la densité de matière.
Einstein calcule le premier modèle d'univers relativiste
En 1917, Einstein calcule le premier modèle d'univers relativiste. Sa grande nouveauté est de proposer une approche entièrement nouvelle de la question de l'espace fini ou infini. Comme Riemann, il veut un univers clos (c'est-à-dire de volumevolume et de circonférence parfaitement finis et mesurables) et sans frontière, aussi choisit-il l'hypersphère pour modéliser la partie spatiale de l'univers.
Avec cet article inaugural de la cosmologiecosmologie moderne, Einstein a conscience de s'aventurer en terrain nouveau. Il prend en effet le contre-pied de la philosophie positiviste illustrée par l'affirmation de Kant : « Aucune observation ne saurait confirmer la thèse de la cosmologie rationnelle, dont l'objet dépasse toute expérience possible ». C'est précisément ce que bat en brèche le modèle d'Einstein : « La question de savoir si le monde est spatialement fini ou non me paraît être une question qui a un sens en géométrie pratique. Il ne me semble même pas exclu que l'astronomie trouve une réponse à cette question dans un avenir relativement proche ». Et Einstein prend nettement parti pour un univers spatialement fini, afin de ne pas être en contradiction avec l'hypothèse de Mach sur l'inertieinertie des corps : « Je ne voudrais pas manquer de rappeler qu'on peut avancer une raison théorique en faveur de l'hypothèse de la finitude de l'univers. La théorie de la relativité générale nous apprend que l'inertie d'un corps déterminé est d'autant plus grande qu'il y a plus de massesmasses pondérables dans son voisinage ; il semble donc parfaitement naturel d'attribuer l'effet d'inertie total d'un corps à l'interaction entre celui-ci et les autres corps de l'univers ; de même que la pesanteur est, depuis NewtonNewton, entièrement attribuée à une interaction des corps entre eux. On peut déduire des équations de la théorie de la relativité générale que cette explication de l'inertie par la seule interaction entre les masses -- telle que par exemple Ernst MachErnst Mach l'appelait de ses vœux -- suppose nécessairement un univers spatialement fini ».
Le modèle d'Einstein fait par ailleurs l'hypothèse d'un univers statique, le rayon de l'hypersphère restant invariable au cours du temps. En vérité, les solutions cosmologiques de la relativité permettent tout à fait d'envisager un espace qui se dilate ou se contracte au cours du temps : c'est ce que démontre le théoricien russe Alexandre Friedmann, entre 1922 et 1924. Le modèle d'Einstein sera abandonné au profit des solutions dynamiques. Mais la nouveauté subsiste : il est possible d'envisager un espace fini et sans borne. Il est d'ailleurs également possible d'envisager un espace infini. La relativité a donc totalement actualisé le dilemme fini ou infini, en mettant à la disposition des cosmologues des espaces explicitement finis ou explicitement infinis.