au sommaire
L'infini constitue-t-il une dimension effective et multiple de la réalité ? Ou bien réside-t-il seulement dans notre esprit, fiction nécessaire à la pensée à quoi nulle réalité physique ne saurait correspondre ? Quelle importance a-t-il en mathématiques ? et en physique ?
Le marcheur, dans la succession de ses pas (un pas, puis un autre, et encore un autre), saisit que sa marche peut se répéter indéfiniment. En principe, il peut toujours faire un pas de plus.

L'infini potentiel
Cette répétition sans limitation conduit à l'intuition première d'un indéfini sans fin : c'est l'infini potentiel, faculté d'aller toujours un peu plus loin. Il est naturellement lié à la notion de successeur d'un entier naturel : 1, 2, 3, etc. À un nombre succède toujours un autre nombre, et il n'en existe pas de dernier, car ce dernier nombre a un successeur. C'est le principe de la récurrence, processus fondamental générateur de l'infini potentiel.
Mais alors, énoncer le 2 préfigure déjà l'infini potentiel. Car 2 = 1 + 1, et rien n'empêche d'écrire ensuite 2 + 1 = 3, 3 + 1 = 4, ad infinitum. Un c'est l'unité ; deux c'est déjà le divers, la multiplicité. Si 2 implique déjà l'infini, cela signifie-t-il que la multiplicité, le divers, sont eux-mêmes potentiellement infinis ?
On le voit, le problème de l'infini concerne autant la philosophie (et la théologie, l'art, l'éthique...) que les sciences de la nature. Encore faudra-t-il distinguer entre les sciences de l'univers, les sciences de la matière et les sciences du nombre, c'est-à-dire les mathématiques.
L'infini chez Aristote
Chez AristoteAristote, le mot « infini » était associé à l'expression de l'imperfection. À sa suite, les scientifiques (et plus encore les philosophes et les théologiens) ont fait preuve, au cours des siècles, d'une résistancerésistance acharnée à l'idée d'infini actuel, au-delà de toute position rationnelle. Les premiers pères de l'Église chrétienne, les néoplatoniciens et les scolastiques le considéreront d'abord comme attribut de Dieu.
Il s'acheminera ensuite de la théologie vers les mathématiques et la philosophie de la nature, s'exprimant à propos de la géométrie perspective (XVe siècle), des infiniment grands de la cosmologie (XVIIe siècle) et des infinitésimaux (XVIIe et XVIIIe siècles). Les infinis deviendront ainsi concevables avant d'être proprement fondés et classés, cette dernière étape relevant des mathématiques et de la logique et occupant les deux siècles qui nous précèdent.
L'infini en mathématiques
Tandis que le physicienphysicien cherche généralement à évacuer l'infini de ses théories, toutes les mathématiques sont arc-boutées sur le concept d'infini. Celui-ci se rapporte en effet à la notion de nombre et à celle d'ensemble. Existe-t-il un nombre que l'on puisse associer à la notion d'infini ? Existe-t-il des ensembles contenant un nombre infini d'éléments ? Nous formulons ici ces questions d'une manière quelque peu naïve car nul n'est capable de dire vraiment ce que veut dire « exister » en mathématiques : les nombres existent-ils en dehors de nous, dans un autre niveau de réalité ? Toujours est-il que les infinis sont source de paradoxes qui ont empêché pendant deux mille ans la constitution d'une théorie permettant leur manipulation. Parmi ces paradoxes, les plus frappants furent celui des indivisibles (à propos des infiniment petits) et celui de la réflexivité (à propos des infiniment grands). En fait, ces deux infinis apparaissent indissolublement liés : dans la partie la plus infime d'une longueur, par exemple, il semble que l'on puisse trouver un nombre infiniment grand de points, de dimension infiniment petite.
L'omniprésence de l'infini en mathématiques est étonnante, car l'Homme est un être fini, limité, embarqué sur une planète limitée et finie. Pourtant, cet être fini examine l'infini et en joue, au point que l'infini lui est indispensable pour appréhender le fini. Un exemple immédiat est le calcul du nombre π, rapport entre la circonférence d'un cercle et son diamètre. Il s'agit d'une longueur finie, mais son expression est un nombre comportant une infinité de décimales. Pour calculer ce nombre (ArchimèdeArchimède l'avait déjà tenté), il faut utiliser un processus infini.
C'est le mathématicienmathématicien Bernard Bolzano qui, au début du XIXe siècle, a proposé pour la première fois pour l'infini un statut équivalent à celui du fini. À la fin du même siècle, les travaux de Georg CantorGeorg Cantor, aujourd'hui considérés comme à l'origine des mathématiques modernes, furent rejetés avec horreur par les scientifiques ; Georg Cantor se battit seul, jusqu'à en perdre la raison.
L'infini en physique
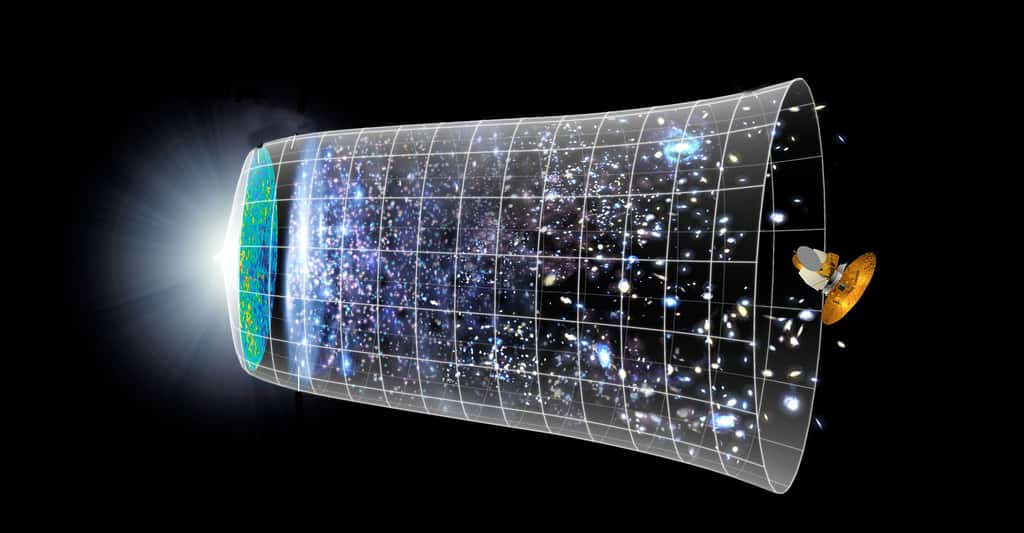
Par ricochet, il a fallu attendre le début du XXe siècle pour une réhabilitation (partielle) de l'infini dans la physique. La théorie quantique, la cosmologie relativiste ou les modèles de trous noirs, par exemple, ont fait surgir de nouveaux infinis. Depuis, fini et infini se côtoient au sein des mêmes modèles.
Au-delà de l'histoire (indispensable, car nul ne peut comprendre l'objet d'une science s'il n'en connaît pas l'histoire), nous voulons repenser « l'actualité de l'infini », l'infiniment grand et son jumeaujumeau l'infiniment petit, à la lueur des théories modernes. Nous prétendons notamment montrer que la cosmologie relativiste reste le seul domaine de la physique d'où l'infini « actuel » (infinité de l'espace, éternité du temps) n'ait pas été éliminé, ce qui reflète sa position épistémologique particulière au sein des autres sciences. Quant aux développements les plus récents de la physique (topologie de l'espace-tempsespace-temps, renormalisation, vide quantique, théorie des supercordesthéorie des supercordes, cosmologie quantique), ils font sans cesse renaître l'infini de ses cendres, tel un sphinx énigmatique aux multiples visages...