L'ensemble des théories de l'infiniment petit et donc des premiers instants de l'Univers ne sont que des théories effectives qui dépendent d'un petit nombre de paramètres effectifs. Rappelons leurs différents types.

La sonde Pioneer. © Don Davis CCO
Les constantes de couplages sont des nombres purs sans dimension physique (elles ne s'expriment pas en fonction des unités de mesure du système SI). Nous avons vu que ces couplages ne sont pas immuables mais dépendent de l'échelle d'énergie à laquelle on mesure, observe ou étudie des phénomènes physiques mettant en jeu l'interaction dont elles mesurent l'intensité. Cette dépendance en l'énergie est logarithmique.
La deuxième classe de paramètres pertinents comprend les masses des particules. Certaines particules comme les fermions ont des masses qui dépendent logarithmiquement de l'énergie. C'est le cas des particules du modèle standardmodèle standard. Par contre, les champs scalaires comme le boson de Higgsboson de Higgs ne possèdent pas cette propriété. En fait, la masse de ces particules reçoit des corrections quantiques à chaque fois qu'une autre particule avec laquelle le champ scalaire interagit à une masse trop grande. C'est-à-dire que la masse de cette particule excède l'énergie des phénomènes décrits par la théorie effective. Dans ce cas, on dit que la particule considérée découple. Par exemple le quark topquark top de masse aux environs de 175 GeVGeV est découplé de la physique nucléaire dont les phénomènes ont lieu à des énergies de l'ordre de 1 GeV. Ainsi la masse d'un champ scalaire à l'énergie peut se décomposer en :
où est la masse du champ scalaire à haute énergie
et la sommation porteporte sur toutes les particules qui ont découplé. Les coefficients
dépendent du modèle considéré. Cette dépendance des masses des scalaires à basse énergie en la masse de particules à haute énergie est une catastrophe. Supposons que
soit petit par rapport à l'échelle
, rien ne garantit que cela reste le cas à basse énergie
quand toutes les masses mi sont plus grandes que
! Pour illustrer ce problème de hiérarchie d'échelle, considérons le modèle standard et sa particule de Higgs. C'est un champ scalaire dont la masse doit être plus petite que 1 TeV pour que le modèle soit cohérent. C'est pourquoi la découverte du champ de Higgs au LHCLHC est attendue. Or ce champ de Higgs est un scalaire. Sa masse dépend donc de toute l'histoire de l'univers depuis les très hautes énergies, à priori depuis l'échelle de PlanckPlanck. Les corrections quantiques nous disent alors que sauf annulation des termes de la somme
la masse du champ de Higgs devrait être de l'ordre de la masse de Planck ! Ceci est hors de question dans le modèle standard.
Ce problème de hiérarchie est connu depuis une trentaine d'années et motive presque toute la recherche des extensions du modèle standard. Deux types d'approches ont été proposés. Nous les avons déjà rencontrées lors de la présentation des différentes théories de la matière noirematière noire. La première repose sur la notion de supersymétriesupersymétrie. Dans le MSSM introduit précédemment, les contributions quantiques arrivent par paires et proviennent d'un boson et d'un fermion de même masse mi. De plus les coefficients associés à ces deux particules se compensent exactement et donc :
lorsque la supersymétrie n'est pas brisée.
Ce résultat permet de préserver la petite masse du Higgs. Bien sur la supersymétrie n'est pas une symétrie exacte de la nature car aucun super-partenaire n'a jamais été observé. Il n'empêche, la contribution des corrections quantiques dépend de l'échelle de brisure de supersymétrie Ms que l'on doit donc prendre de l'ordre de 1 TeV pour conserver les propriétés du modèle standard.
Une autre approche est plus radicale et suppose que vers une énergie de quelques TeV, une nouvelle dimension d'espace s'ouvre. Dans ce cadre, les propriétés quantiques des théories avec dimensions supplémentaires peuvent résoudre le problème de hiérarchie.
Ainsi, le problème de hiérarchie de masse peut être résolu au prix d'introduire de nouvelles structures physiques à l'échelle du TeV. C'est pour cela que les résultats du LHC sont attendus avec impatience. Les physiciensphysiciens espèrent que la nouvelle physique décrite dans cette section, et ses applicationsapplications cosmologiques à la matière noire, y seront découvertes.
L'approche de la physique de l'infiniment petit par les théories effectives est sérieusement mis en échec par une découverte qui a eu lieu en 1998 : l'accélération de l'expansion de l'Universaccélération de l'expansion de l'Univers. Revenons pour cela aux découvertes faites par Slipher puis par Hubble. Depuis les années trente, nous savons que l'univers n'est pas statique mais est en expansion. Cela se traduit par une dépendance temporelle du facteur d'échelle a(t). Sous l'effet de la gravite qui est attractive, il était admis que ce facteur d'échelle devait augmenter peu et même voir son taux d'accroissement décroître avec le temps.
Depuis Hubble, les astrophysiciensastrophysiciens s'intéressent à la dynamique d'objets lointains qui agissent comme des traceurs de l'expansion. Les meilleurs de ces objets sont les supernovaesupernovae de type Ia. Ces astresastres explosent et disparaissent d'une façon qui est bien mesurée. De ces explosions, il est possible de mesurer leur luminositéluminosité et de ce fait leur distance. De même l'observation de leurs spectres d'émissionspectres d'émission lumineuse permet de connaître leur vitessevitesse (ou encore le décalage vers le rougedécalage vers le rouge des raies lumineuses par effet Dopplereffet Doppler). A partir de ce diagramme dit de Hubble, il est possible d'extraire l'accélération de l'Univers, c'est-à-dire la deuxième dérivée temporelle du facteur d'échelle. La grande surprise est que cette deuxième dérivée est positive et que donc l'univers a une expansion accélérée ! Le contraire de ce qu'un univers rempli de matière devrait engendrer. Cette énigme trouve sa solution grâce à une vieille idée d'EinsteinEinstein : la constante cosmologiqueconstante cosmologique.
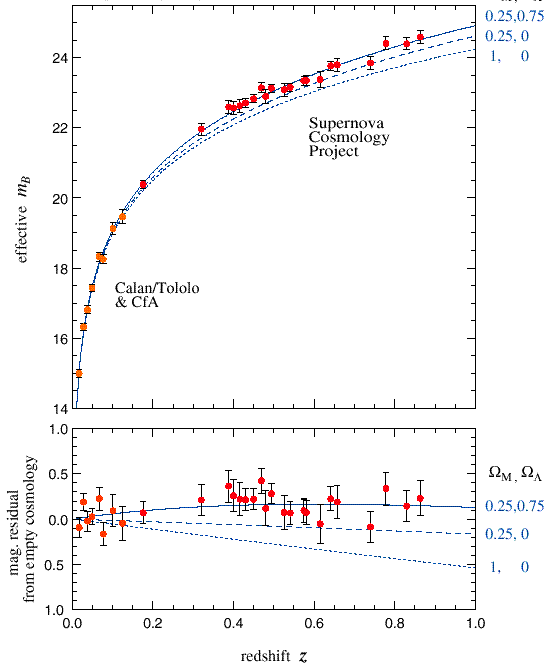
Le diagramme de Hubble des supernovae de type Ia montrant l’accélération de l’expansion de l’univers. Ce diagramme donne la distance en fonction du décalage vers le rouge z.
Pour mieux comprendre comment une accélération de l'expansion peut être modélisée, il est utile de considérer une analogieanalogie thermodynamiquethermodynamique. Imaginons un fluide de densité d'énergie constante, c'est-à-dire d'énergie par unité de volumevolume constante. Augmentons le volume d'en petit élément dV, la variation de l'énergie interneénergie interne est dU=
dV. Cette variation est identifiée avec le travail dU=-pdV, d'où l'on déduit qu'un fluide de densité d'énergie constante est tel que :
Cette relation s'appelle l'équationéquation d'état du fluide. Elle nous enseigne que ce fluide a une pressionpression négative, c'est ce type de fluide que représente une constante cosmologique. La constante cosmologique est associée à une densité d'énergie constante et à une pression négative. En relativité généralerelativité générale, une pression négative contrecarre l'attraction gravitationnelle et peut donner lieu à une expansion accélérée.
Pour ce faire il faut que la constante cosmologique soit plus grande que la densité d'énergie de la matière. En fait, il a été observé que 5% du contenu de l'Univers est composé de baryonsbaryons, 25% de matière noire et 70% correspondent à la constante cosmologique. La densité d'énergie associée dite énergie du vide vaut :
Cette valeur correspond à une densité de 10-29 g /cm3 ! Elle est si petite qu'il est difficile de la comprendre. C'est d'autant plus vrai que la valeur de l'énergie du vide reçoit des corrections quantiques comme les masses des scalaires. L'énergie du vide est un des paramètres pertinents des théories effectives. Ces corrections apparaissent comme :
Ceci conduit au plus sérieux problème de hiérarchie de la physique actuelle. En effet, il n'existe aucun mécanisme connu (même pas la supersymétrie) qui permet de garantir qu'à très basse énergie, bien après la formation des atomesatomes , l'énergie du vide soit si petite alors qu' elle reçoit des contributions venant de la physique qui peut aller jusqu' à l'échelle de Planck , soit quelques 120 ordres de grandeurordres de grandeur de plus que la valeur observée. Bien sûr, il est envisageable que les termes de la somme donnant la valeur de l'énergie du vide à basse énergie s'annulent de façon fortuite. En l'absence de toute explication, cette possibilité semble peu probable. Pour cette raison, certains physiciens avancent que la petite valeur de l'énergie du vide a une origine anthropique.
En effet, il existe une borne due à Weinberg qui stipule que si l'énergie du vide excède l'énergie de la matière de plus de 500 fois, il est impossible de former des galaxiesgalaxies et donc a fortiori des physiciens pour mesurer l'énergie du vide. Ce type d'argument reposant sur le fait qu'il existe des observateurs, dont la simple existence contraint les processus physiques ayant eu lieu dans l'Univers, porte le nom d'anthropique.
Maintenant, il semblerait que la théorie des cordesthéorie des cordes prédise qu'une multitude d'univers soit possible, chacun avec sa propre histoire et ses propres caractéristiques. Les partisans de l'approche anthropique assertent que, dans cet ensemble, il doit en exister un tel que l'énergie du vide est celle observée. Ce type d'arguments conduit à de nombreux débats car il tend à récuser toute tentative de compréhension fine de la petite valeur de l'énergie du vide.
Le problème de la constante cosmologique clôt notre cheminement dans les théories de l'infiniment petit et leurs liens avec la cosmologiecosmologie. Il existe d'autres approches au problème de la constante cosmologique. Toutes mettent en exergue le fait qu'il s'agit d'un manque de compréhension de la nature du vide et de ses effets gravitationnels. Il se pourrait que la gravitégravité doive être modifiée à grande distance et que ce qui est interprété comme accélération devrait être vu comme modification de la loi de Newton aux échelles cosmologiques. Malheureusement, il est très difficile de construire des modèles de gravité modifiée à longue distance.
Une autre possibilité serait que l'univers ne soit pas homogène mais possèderait de grands vides. Nous serions au centre de ce vide et l'accélération de l'expansion ne serait qu'une illusion due à la différence d'expansion dans des régions sous et sur denses de l'univers. Dans ce cas, le principe de CopernicCopernic serait violé car nous occuperions une place privilégiée dans l'univers.
L'échec des théories effectives dans la description de l'énergie du vide est si sérieux que les physiciens examinent de nombreuses pistes et sont prêts à remettre en cause certains principes fondamentaux.
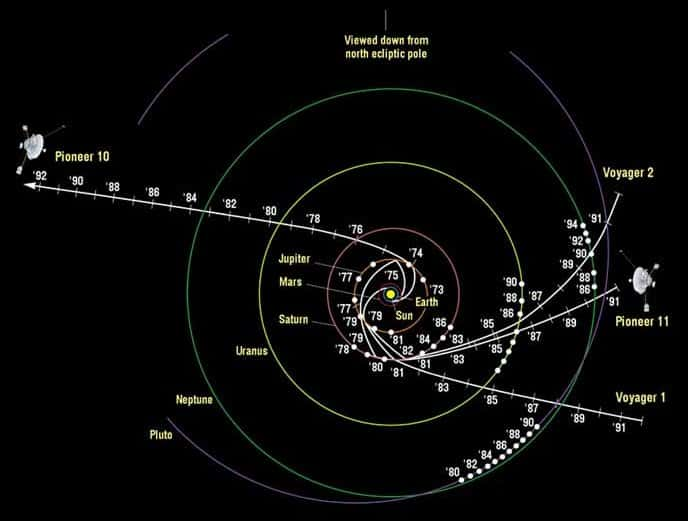
La sonde Pioneer a subi une accélération anormale constante et dirigée vers le Soleil lors de son voyage vers les confins du système solaire. Aucune explication à ce phénomène n’est connue. Crédit : Newscientist-Nasa.
Mais avant de le faire, il est bon de se remémorer que la gravité est un objet délicat, que sa compréhension est toujours en constructionconstruction et que même dans le système solairesystème solaire il existe des anomaliesanomalies sans explications à l'heure actuelle. Ainsi la sonde Pioneer dans son voyage vers les régions hors du système solaire a subi une petite accélération constante vers le soleilsoleil qu'aucun phénomène physique n'explique.
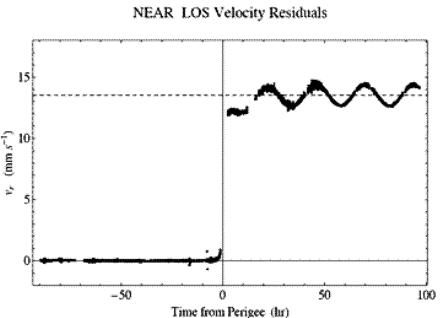
Certains satellites avec des orbites passant très près de la terre avant de s’en éloigner sur des orbites hyperboliques ont eu subi un saut de vitesse au passage par leur périgée. Cette non-conservation de l’énergie est un mystère.
Certaines anomalies, comme celle de l'avance de périhéliepérihélie de Mercure, ont été expliquées par la relativité générale. Peut-être que ces anomalies nous apprendrons si la relativité générale doit être modifiée et si cette modification permet de résoudre le problème de la constante cosmologique.






























