Calcul du centre latéral de poussée

N.B. : cette page est en cours de réécriture.

1. Méthode

Comme nous l'avons vu plus haut, tous les éléments extérieurs de la fuséefusée, à l'exception des cylindres qui forment le corps de la fusée, sont à prendre en compte pour calculer précisément la position du centre latéral de poussée.

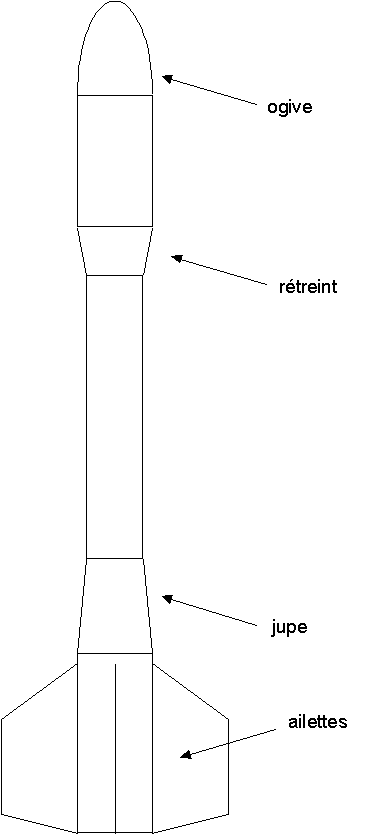
Les différents éléments à considérer

La méthode consiste, pour chacun des éléments, à déterminer son centre latéral de poussée propre, ainsi qu'un coefficient pondérateur. Ainsi, pour l'ogive, la ou les jupe(s), le ou les rétreint(s), la ou les séries d'ailettes, on calcule un X_{CLP élément} et un C_élément. Ensuite, une formule de type barycentrique permet de déterminer le X_CLP de la fusée.

2. L'ogive

Trois formes d'ogive seront considérées :

• Ogivale (définition architecturale),
• Parabolique (plus précisément, paraboloïdale de révolution),
• Conique.

Le critère dimensionnel est sa hauteur I_ogive.

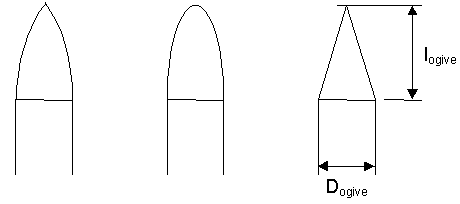
Ogives ogivale, parabolique et conique

Le coefficient ne dépend pas de la forme de l'ogive. Le X_{CLP ogive} vaut entre 0.47 et 0.67 fois la hauteur de l'ogive, ce qui est une variation assez faible. Le choix de l'ogive n'est donc pas un élément important dans la conception globale et, en tout cas, pas un moyen de déplacer sur une grande envergure le X_CLP global de la fusée.

On constatera que le diamètre D_ogive n'intervient pas. En fait, il servira de référence pour le calcul des jupes et rétreints.

3. Les jupes

Les jupes sont considérées coniques. Elles sont caractérisées, au niveau dimensionnel, par leurs deux diamètres d et D, leur hauteur l_jupe et leur distance au sommet de la fusée L_jupe :

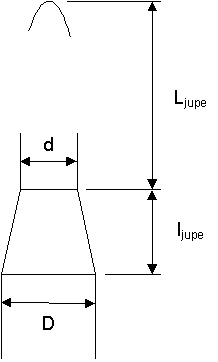
Cotation de la jupe

4. Les rétreints

Les rétreints sont aussi considérés comme coniques. Ils sont caractérisés, au niveau dimensionnel, par leurs deux diamètres d et D, leur hauteur I_rétreint et leur distance au sommet de la fusée L_rétreint :

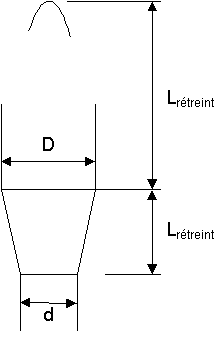
Cotation du rétreint

5. Les ailettes

On considérera deux cas pour le calcul de la position et du coefficient du centre latéral de poussée :

• Les ailettes classiques, c'est à dire conforme au schéma ci-dessous,
• Les ailettes non conventionnelles, c'est à dire de morphologiemorphologie plus complexe que l'ailette du schéma ci-dessous. Dans ce cas, les formules sont issues des études et expérimentations qui j'ai réalisées (fusées de la série Ozone).

Considérons déjà le cas le plus courant de l'ailette "classique".

1. Les ailettes simples

Définissons tout d'abord les "bords" des ailettes :

• Bord d'attaque (ou bord supérieur) : côté de l'aileron soumis au ventvent relatif,
• Bord de fuite (ou bord inférieur) : opposé au bord d'attaque,
• Bord interne : solidarisé au corps de la fusée,
• Bord externe : opposé au bord interne.

Définissons maintenant les côtes caractéristiques :

• L_ailette : distance du sommet de la fusée au haut du bord interne,
• D_ailettes : diamètre du corps de la fusée au niveau des ailettes,
• m : longueur du bord interne,
• n : longueur du bord externe,
• p : longueur du bord d'attaque projeté sur l'axe de la fusée,
• e : distance du bord interne au bord externe,
• f : distance du mi-bord interne au mi-bord externe,

• Q : nombre d'ailettes.

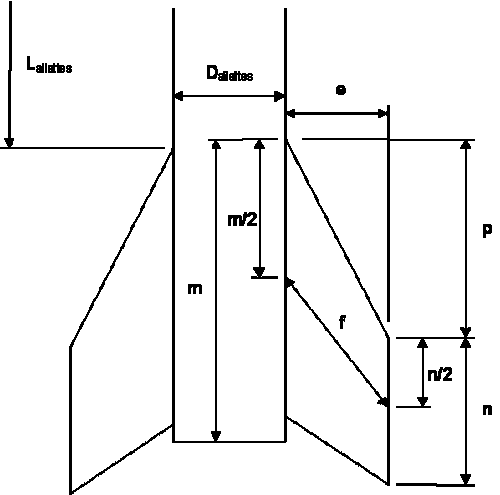
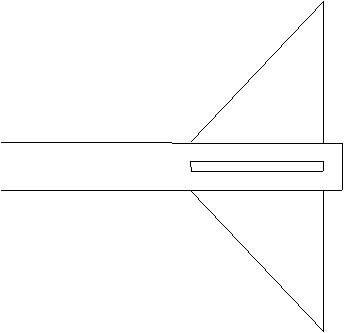
Cotation des ailettes

Cette modélisation permet de nombreuses formes d'ailettes. Par exemple, avec respectivement :

• n = 0 et p = m,
• p = (m - n)/2,
• p = 0 et m =n,
• n = 0, p > m,

On obtient :

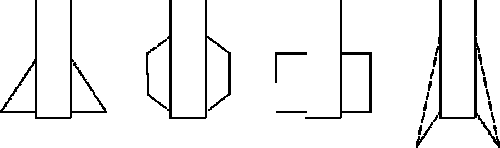
Différentes formes d'ailettes

Le nombre d'ailettes Q ne doit pas être choisit au hasard :

• Q = 1 : impossible (manque de symétrie),
• Q = 2 : impossible (manque de symétrie centrale),
• Q = 3, 4 : cas les plus courants,
• Q = 5, 6 : cas plus rares
• Q > 6 : à éviter, risque de sortie du domaine de validité des formules.

2. Séries multiples et décomposition

Il est tout à fait possible d'implanterimplanter sur une fusée plusieurs séries d'ailettes. Il suffira d'en tenir compte dans le calcul du XCLP final. On peut retenir cette méthode dans le cas où une fusée est appelée à voler dans deux configurations de masse ou de géométrie différentes. La première série d'ailettes, principale, sera alors calculée pour une des deux configurations et la seconde série, ajoutée à la première sera alors calculée pour que l'ensemble de la fusée, en seconde configuration, continue à respecter la condition de stabilité. Cette possibilité de considérer deux séries d'ailettes peut aussi être utilisée en sens inverse : elle permettra alors de calculer l'effet d'une seule série d'ailettes, mais dont la géométrie n'est pas conforme à la décomposition ci-dessus. Par exemple, les ailette ci-dessous ne suivent pas la modélisation, mais il est possible de les diviser en deux ailettes qui, elles, sont conformes à la modélisation :

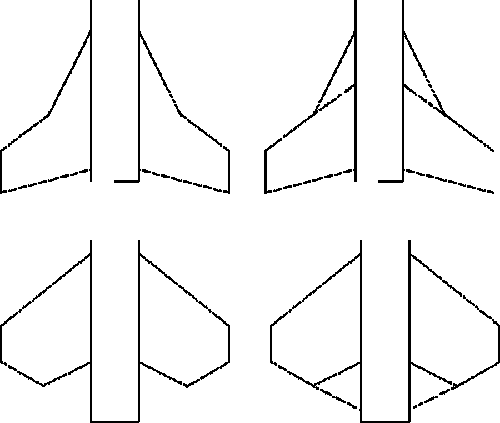
Exemples de décomposition

Dans le premier exemple, on peut décomposer en deux ailettes dont la somme est égale à l'ailette de départ. Dans le second exemple, on peut décomposer en deux ailettes dont la différence (la grande moins la petite) est égale à l'ailette de départ. On affectera alors d'un signe moins le coefficient de l'ailette à soustraire. Attention, dans ces deux cas, les deux L_ailettes ne sont pas les mêmes pour les deux séries. 3. Ailettes plus évoluées Malgré l'astuce de décomposition des ailettes, il n'est pas toujours possible de modéliser, et donc de calculer certaines formes d'ailettes. Comment alors faire si, comme moi, on a l'imagination un peu trop débordante. Comme expliqué plus haut, je me suis penché assez profondément sur ce problème et de mes réflexions sont issues des "extensions" aux formules ci-dessus, lesquelles ont été validées par des expérimentations grandeur nature. Voici les résultats que j'ai obtenus : Ailette cylindrique concentrique

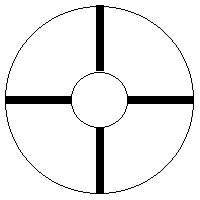
Vue axiale

Cet exemple se traite en deux parties, selon la méthode de décomposition évoquée ci dessus : les quatre ailettes classiques (nombre au choix du concepteur), que l'on calculera selon la méthode ci-dessus, et un cylindre, que l'on modélisera de la façon suivante :

• D_ailette : diamètre de la fusée,
• D_cylindre : diamètre du cylindre,
• H_cylindre : hauteur du cylindre.

On utilise alors les formules des ailettes avec :

• m = H_cylindre,
• n = H_cylindre,
• p = 0,
• e = (D_cylindre - D_ailette)/2,
• f = (D_cylindre - D_ailette)/2,
• Q = 3

Ailettes cylindriques déportées

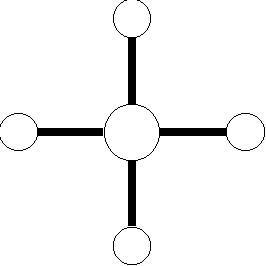
Vue axiale

Note : les cylindres déportés sont creux. Cet exemple se traite en deux parties, selon la méthode de décomposition évoquée ci dessus : les quatre ailettes classiques (nombre au choix du concepteur), que l'on calculera selon la méthode ci-dessus, et les cylindres, que l'on modélisera de la façon suivante :

• D_ailette : diamètre de la fusée,
• D_cylindre : diamètre des cylindres,
• H_cylindre : hauteur des cylindres,
• Q : nombre de cylindres,
• k : largeur des ailettes de maintien.

On utilise alors les formules des ailettes avec :

• m = H_cylindre,
• n = H_cylindre,
• p = 0,
• e = D_cylindre,
• f = D_cylindre