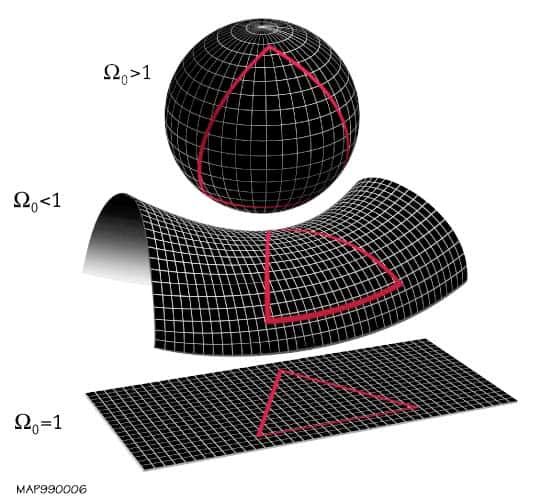
En cosmologie relativiste, on introduit un paramètre Ω0 qui est le rapport de la densité d'énergie mesurée dans l'univers observable et de la densité critique dans le cadre des univers homogènes et isotropes. Lorsque la densité est supérieure à la densité critique (Ω0 > 1), la géométrie spatiale de l'univers observable est celle d'une sphère. Lorsque Ω0 < 1, on est dans en présence d'un univers ouvert, et lorsque Ω0 = 1, la géométrie spatiale est plate.
En cosmologie, la densité critique correspond à la densité d'énergie que l'on doit avoir dans le cadre des modèles relativistes d'univers homogènes et isotropesisotropes en expansion pour que la courbure spatiale y soit nulle. Les lois de la géométrie euclidienne, donc plane, y sont valables.
Densité critique et différentes courbures de l’espace
Lorsque la densité est inférieure à la densité critique, on est dans le cadre d'un univers ouvert. La géométrie est déterminée par une courbure négative, comme celle d'une selle de cheval.
Lorsque la densité est supérieure à la densité critique, on est dans le cadre d'un univers clos, car de taille finie dans l'espace. La géométrie est déterminée par une courbure positive, comme celle d'une sphère.
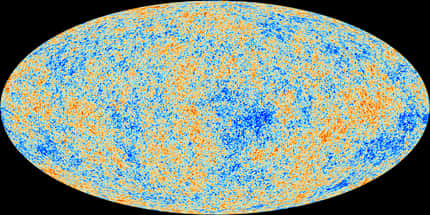
La densité massique critique correspond à une densité de quelques atomesatomes par mètre cube. La courbure spatiale de l'univers observable est très faible, donc très proche de sa densité critique. Il ne faut pas perdre de vue que la densité de l'univers observable actuel est dominée par l'énergie noireénergie noire et la matière noire. Il y a donc en réalité moins d'un atome par mètre cube.