au sommaire
La deuxième loi de Keplerloi de Kepler, également connue sous le nom de « loi des aires », est l'une des trois lois énoncées par l'astronomeastronome et mathématicienmathématicien allemand Johannes Kepler (1571-1630), au début du XVIIe siècle pour décrire le mouvement des planètes autour du Soleil.
Contexte historique de la deuxième loi de Kepler
Le contexte historique de la formulation de cette loi s'inscrit dans une période charnière marquée par le déclin du modèle géocentriquegéocentrique de PtoléméePtolémée (théorie qui place la terre immobile au centre du monde) et l'émergenceémergence du modèle héliocentriquehéliocentrique de Copernic (théorie qui place le soleil au centre de l'univers). Les observations astronomiques de Tycho Brahe, qui a minutieusement mesuré les positions des planètes, ont fourni à Kepler les données nécessaires pour développer ses lois.
Kepler a formulé ces lois à partir de l'observation méticuleuse des mouvements planétaires et a construit ainsi un cadre mathématique qui a jeté les bases du modèle héliocentrique de notre Système solaire.
La deuxième loi de Kepler a été publiée pour la première fois en 1609 dans son ouvrage Astronomia Nova. L'idée révolutionnaire que les planètes ne suivaient pas des orbites circulaires parfaites mais plutôt des orbites elliptiques avec des vitessesvitesses variant au cours de leur mouvement, a été fondamentale pour le développement ultérieur de la mécanique céleste et a jeté les bases des travaux ultérieurs, notamment ceux de Sir Isaac Newton.
Énoncé de la deuxième loi de Kepler
La deuxième loi de Kepler décrit le comportement du mouvement orbital des planètes. Elle énonce que, lorsqu'une planète se déplace autour du Soleil, la ligne qui relie le centre du Soleil à la planète balaie des aires égales en des intervalles de temps égaux. Autrement dit, la vitesse d'une planète varie de manière à ce que la portion d'aire balayée par la ligne reliant la planète au Soleil soit constante pendant son mouvement orbital.
- Énoncé de la deuxième loi de Kepler ou « Loi des aires » : le rayon-vecteur reliant une planète au Soleil balaie des aires (a) égales en des temps égaux (t). Le rayon-vecteur est une droite imaginaire reliant le Soleil, situé à un des foyersfoyers de l'ellipse, à la planète située sur l'ellipse.
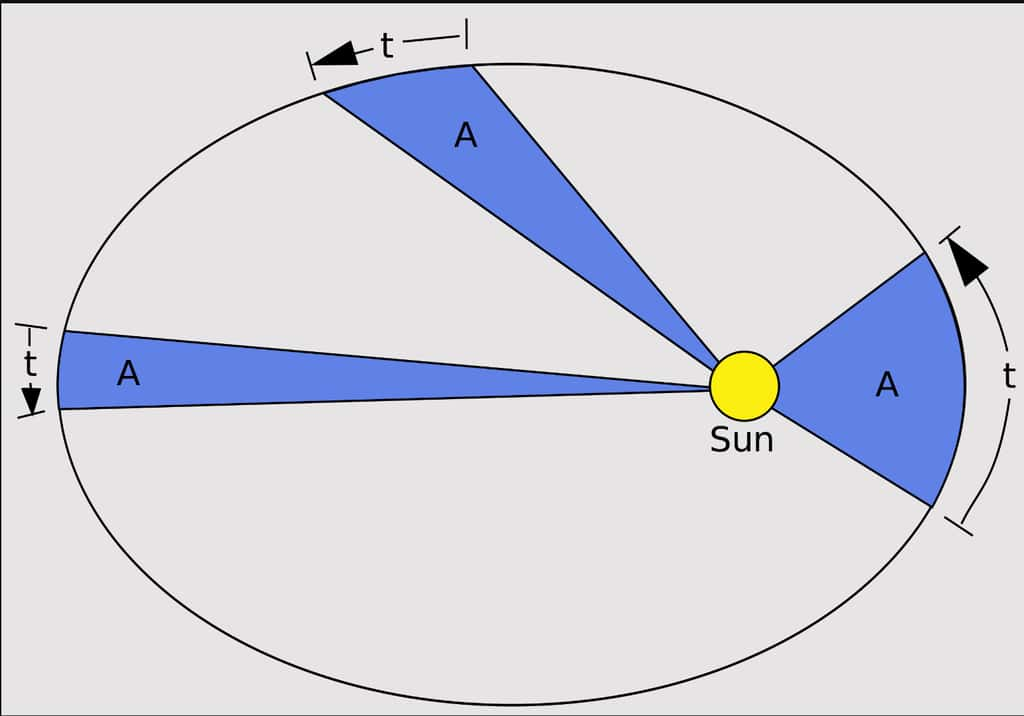
Pour comprendre cela intuitivement, il faut imaginer une planète qui se déplace le long de son orbite elliptique. Si l'on trace une ligne imaginaire entre le centre du Soleil et la planète, cette ligne balaye une certaine surface (aire) dans un intervalle de temps donné. La deuxième loi de Kepler stipule que, quelle que soit la position de la planète sur son orbite, la surface balayée par cette ligne pendant une période donnée reste constante.
Cela signifie que lorsque la planète est plus proche du Soleil (périhéliepérihélie), elle se déplace plus rapidement pour balayer une plus petite surface, compensant ainsi la proximité avec le Soleil. De même, lorsque la planète est plus éloignée du Soleil (aphélieaphélie), elle se déplace plus lentement mais balaye une aire plus grande. Cette deuxième loi permet d'affirmer qu'une planète se déplacera plus rapidement sur son orbite au périhélie qu'à l'aphélie. Ainsi, la loi des aires exprime une sorte d'équilibre dynamique entre la vitesse orbitaleorbitale d'une planète et la forme de son orbite.
La deuxième loi de Kepler dans le Système solaire
La deuxième loi de Kepler se manifeste dans de nombreux mouvements orbitaux dans le Système solaire. Ces exemples démontrent comment la deuxième loi de Kepler est une caractéristique générale des mouvements orbitaux dans le Système solaire. Voici quelques exemples illustrant cette loi :
- Mouvement de la Terre autour du Soleil : l'orbite de la Terre autour du Soleil offre un exemple classique de la deuxième loi de Kepler. Lorsque la Terre est plus proche du Soleil (périhélie), elle se déplace plus rapidement, balayant une aire plus petite en des intervalles de temps égaux. À l'inverse, lorsqu'elle est plus éloignée du Soleil (aphélie), elle se déplace plus lentement, mais balaye une aire plus grande. Cette variation de vitesse orbitale assure que la loi des aires est respectée.
- Mouvement de Mars autour du Soleil : les observations de la planète Mars confirment également la deuxième loi de Kepler. L'orbite elliptique de Mars montre une variation significative de sa vitesse orbitale, en accord avec la loi des aires.
- Mouvement des satellites autour de la Terre : la deuxième loi de Kepler n'est pas limitée aux planètes. Elle s'applique également aux satellites en orbite autour de la Terre. Les satellites en orbite basse ont une vitesse orbitale plus élevée que ceux en orbite plus éloignée. Ainsi, ils balayent des aires plus petites en des intervalles de temps égaux.
- Les anneaux de Saturneanneaux de Saturne : même si les particules constituant les anneaux de Saturne ne sont pas des objets massifs individuels, la deuxième loi de Kepler peut être observée à l'échelle des particules individuelles dans ces anneaux. Les parties intérieures des anneaux se déplacent plus rapidement que les parties extérieures, maintenant la constance de l'aire balayée.
- ComètesComètes en orbite autour du Soleil : les comètes, avec leurs orbites souvent très excentriquesexcentriques, illustrent également la deuxième loi de Kepler. Lorsqu'une comète s'approche du Soleil, sa vitesse orbitale augmente, et elle ralentit à mesure qu'elle s'éloigne.