On appelle trigonométrie -- du grec trigonos signifiant triangulaire et métron, mesure --, la branche des mathématiques qui fait le lien entre les distances et les angles dans les triangles. Elle étudie également le comportement des fonctions dites fonctions trigonométriques (sinus, cosinus, tangente).
L'intérêt des civilisations pour la trigonométrie semble remonté à quelque 4.000 ans. Ses résultats ont d'abord servi la navigation et l'astronomie et aujourd'hui encore, les principes de la trigonométrie apparaissent dans de nombreux champs des sciences : physiquephysique, électricité, mécanique, économie, biologie, géographie, etc.
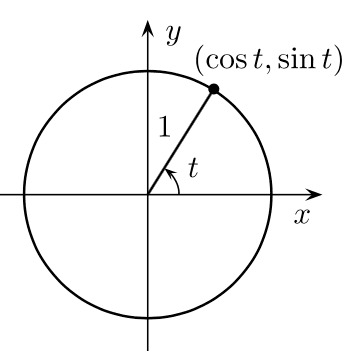
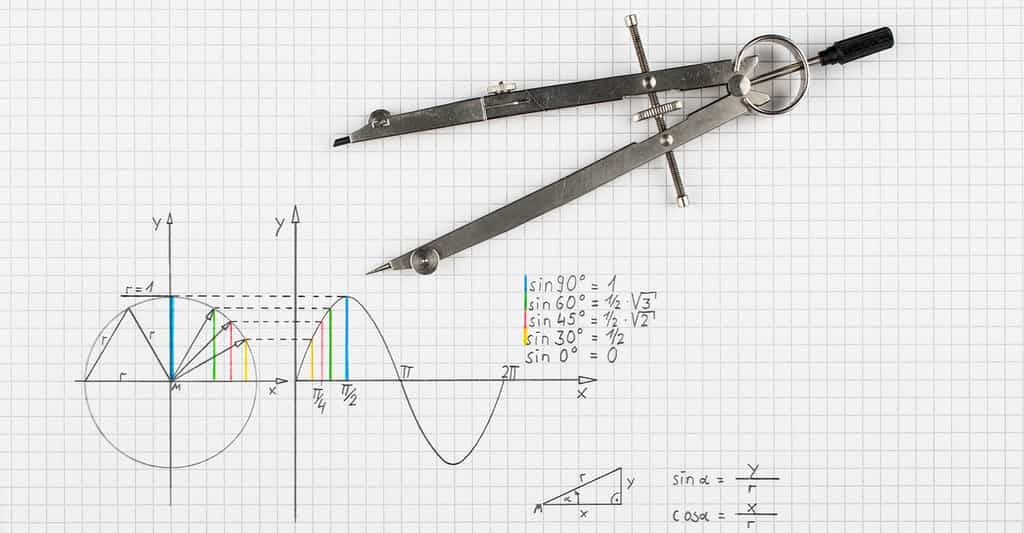
En trigonométrie, les coordonnées d’un point M situé sur un cercle de rayon 1 — le cercle trigonométrique — sont les suivantes : abscisse = cos t et ordonnée = sin t. © Gustavb, Wikipedia, CC by-SA 3.0
Quelques formules trigonométriques
Pour définir les fonctions trigonométriques, on peut s'appuyer sur un triangle rectangle, un triangle qui présente un angle droit, un angle mesurant 90°. Nommons-le A. Les autres angles étant nommés B et C. Le côté opposé à cet angle est alors baptisé hypoténuse. Nommons-la a. Et nommons b et c, les côtés respectivement opposés à B et C. Les fonctions cosinus, sinus et tangente sont alors définies comme suit :
cos B = c / a ; sin B = b / a ; tan B = b / c
À côté de ces définitions existe une foule de formules trigonométriques qui permettent de résoudre un triangle, c'est à dire, à partir de la donnée d'un côté et de deux angles adjacents, par exemple, de déterminer toutes les grandeurs manquantes.
Par exemple :
- cos2 B + sin2 B = 1
- cos (B+C) = cos B x cos C -- sin B x sin C
- sin (2B) = 2 x sin B x cos B
- sin (B+C) + sin (B-C) = 2 x sin B x cos C
- tan (B-C) = (tan B -- tan C) / (1 + tan B x tan C)