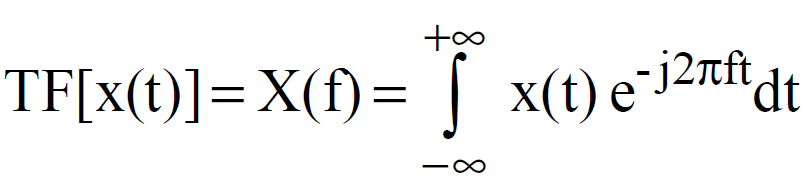au sommaire
La transformée de Fourier est une opération qui permet de représenter en fréquence (développement sur une base d'exponentielles) des signaux qui ne sont pas périodiques. Il s'agit de l'analogue des séries de Fourier pour les fonctions périodiques (développement sur la base de fonctions sinusoïdales). Une fonction non périodique pouvant être considérée comme une fonction dont la période est infinie. Ce passage à la limite nous fait passer des séries aux intégrales.
Applications diverses de la transformée de Fourier
Caractériser un signal par son spectre de fréquence permet notamment de mettre en évidence l'importance de l'harmonique fondamental ainsi que la décroissance plus ou moins rapide de l'amplitude des harmoniques de rang plus élevé. Il peut aussi servir à déterminer le nombre d'harmoniques nécessaires pour transmettre la quasi-totalité de l'énergie du signal (bande passante, coupe-bande...).
Analyse et traitement des signaux
La transformée de Fourier trouve de vastes applications non seulement en physique et en ingénierie, mais également en statistique, en économétrie, en finance, et dans d'autres domaines scientifiques où l'analyse et le traitement des données en fréquence sont nécessaires. Par exemple, en médecine, elle est utilisée pour analyser les signaux d'IRMIRM ou d'ECGECG pour détecter des anomaliesanomalies fonctionnelles ou structurelles.
Décomposition et reconstruction des signaux
Un avantage crucial de la transformée de Fourier réside dans sa capacité à décomposer un signal complexe en composantes fréquentielles simples, ce qui permet une analyse plus facile et plus compréhensible. Ceci est particulièrement utile dans les domaines de la télécommunication pour la compression de données et le filtrage de signal.
Outils mathématiques sous-jacents
Mathématiquement, la transformée de Fourier transforme une fonction temporelle en une fonction fréquentielle en utilisant l'intégrale de Fourier. Ce processus convertit le temps ou l'espace en fréquences, facilitant ainsi l'étude du comportement fréquentiel des signaux.
Importance de la dualité temps-fréquence
- Elle aide à comprendre la structure interne du signal en termes de fréquences constitutives.
- Elle est essentielle dans le diagnosticdiagnostic technique, par exemple, pour identifier les causes des vibrationsvibrations dans les machines et planifier le maintien prédictif.
Complexité et défis
Malgré ses nombreuses applications, la mise en œuvre de la transformée de Fourier peut présenter des défis, notamment en termes de calculs intensifs, surtout pour les grands ensembles de données. L'optimisation des algorithmes et l'utilisation de techniques telles que la Transformée de Fourier Rapide (FFT) sont cruciales pour améliorer l'efficacité des processus.