au sommaire
Le théorème de Pythagore, un théorème de la géométrie euclidienne, doit son nom à un mathématicienmathématicien grec du début du VIe siècle avant J.-C. Et ce même si le résultat qu'il énonce était probablement connu bien plus tôt. C'est en effet à Pythagore qu'en est attribuée la première démonstration. Démonstration dont il ne reste malheureusement aucune trace écrite.
Le théorème de Pythagore s'énonce ainsi : si un triangle est rectangle, alors le carré de la longueur de son hypoténuse -- le côté opposé à son angle droit -- est égal à la somme des carrés des longueurs des deux côtés formant l'angle droit. En d'autres mots, si ABC est un triangle rectangle en B alors : AC2 = AB2 + BC2.
Notez que si dans un triangle, AC2 n'est pas égal à AB2 + BC2, on peut affirmer que ce triangle n'est pas rectangle en B.
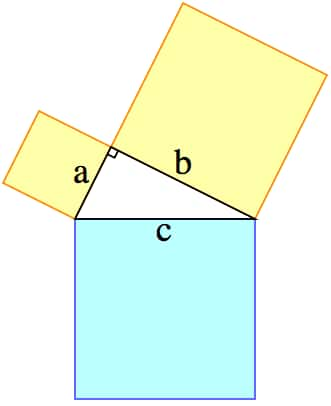
Le théorème de Pythagore nous apprend que l’aire du carré en bleu est égale à la somme des aires des deux autres carrés. © Marianov, Wikipedia, CC0
Une réciproque tout aussi vraie
La réciproque du théorème de Pythagore est également toujours vérifiée. Elle s'énonce ainsi : si dans un triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et on appelle hypoténuse, son plus grand côté. Ou encore, si dans un triangle ABC, AC2 = AB2 + BC2 alors, le triangle est rectangle en B.
Là aussi, notez que si l'on sait qu'un triangle n'est pas rectangle en B, alors on peut également affirmer que AC2 n'est pas égal à AB2 + BC2.
Cette équivalence permet finalement d'affirmer qu'un triangle est rectangle si, et seulement si, le carré de la longueur de son hypoténuse est égal à la somme des carrés des longueurs de ses deux autres côtés.
Triplets pythagoriciens
On qualifie de triplets pythagoriciens, trois nombres entiers qui vérifient la relation de Pythagore. Ainsi (3, 4 et 5) représente le premier des triplets pythagoriciens puisque 52 = 42 + 32.