au sommaire
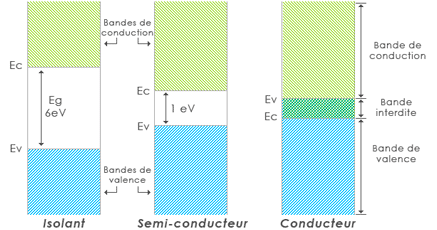
Structure en bande dans un isolant, un semi-conducteur et un solide. Crédits : energies2demain.com, contrat http://creativecommons.org/licenses/by-nc-sa/2.0/fr/
La théorie des bandes est un modèle quantique en physique des solides qui détermine les énergies possibles des électrons dans un solide et permet de comprendre la notion de conductivité électrique. Il est issu de la théorie des orbitales moléculaires.
Dans un solide, les niveaux d'énergie permis sont confinés dans une bande dont la largeur, de l'ordre de l'électronvolt, dépend du cristal et du recouvrement des orbitales atomique.
Les solides ont une structure de bandes ; on distingue les bandes d'énergie permises, et les bandes d'énergie interdites. Les bandes d'énergie se remplissent selon la loi statistique de Fermi : on montre qu'à 0 K, les électrons occupent tous les niveaux d'énergie inférieure à l'énergie de Fermi, ou niveau de Fermi. Sa valeur est caractéristique du cristal considéré.
On met alors en évidence la bande de valence et la bande de conduction.
Origine et principes fondamentaux
La théorie des bandes est élaborée à partir des principes de la mécanique quantiquemécanique quantique, et est précisément une extension de ces principes au cas des électrons dans les cristaux. Cette théorie repose sur le principe que les électrons dans un solide peuvent être modélisés par une fonction d'onde collective qui étend son influence sur l'ensemble du cristal. L'approximation des liaisons fortes et l'approximation des liaisons faibles sont deux méthodes fréquemment utilisées pour évaluer les bandes d'énergie dans un matériaumatériau.
Classification des matériaux selon la théorie des bandes
Selon la structure des bandes d'énergie, les matériaux peuvent être classés en isolants, semi-conducteurssemi-conducteurs ou conducteurs. Cette classification est déterminée par la position relative de la bande de conductionbande de conduction (la plus basse bande d'énergie non remplie) par rapport à la bande de valencebande de valence (la plus haute bande d'énergie remplie) :
- Isolants: Il existe un grand gapgap (intervalle d'énergie interdit) entre la bande de valence et la bande de conduction, empêchant les électrons de gagner assez d'énergie pour contribuer à la conductivitéconductivité électrique.
- Semi-conducteurs: Le gap entre la bande de valence et la bande de conduction est plus petit, permettant aux électrons de passer facilement d'une bande à l'autre sous certaines conditions (par exemple, excitation thermique ou lumineuse).
- Conducteurs (métauxmétaux): La bande de conduction et la bande de valence se chevauchent, ou la bande de conduction est partiellement remplie, permettant aux électrons de se déplacer librement et de conduire le courant électriquecourant électrique.
Applications technologiques de la théorie des bandes
La théorie des bandes est fondamentale dans le développement et l'amélioration des dispositifs électroniques et optoélectroniquesoptoélectroniques, incluant les transistors, les diodes et les cellules solaires. Elle permet également de prédire la couleurcouleur et la transparencetransparence des matériaux, ce qui est crucial pour les technologies d'affichage et les capteurscapteurs optiques.
Des recherches récentes ont exploré les anomaliesanomalies dans la structure de bandes de certains matériaux exotiquesexotiques, comme les isolants topologiques et les semi-métaux de Weyl, qui possèdent des propriétés électroniques uniques dues à la topologie complexe de leurs bandes électroniques. Ces études sont cruciales pour le développement de nouvelles technologies quantiques.
Importance de la modélisation par théorie des bandes dans la science des matériaux
La capacité de modéliser précisément les bandes électroniques des matériaux est essentielle pour la synthèse de nouveaux matériaux avec des propriétés spécifiques désirées. Cette approche permet de prédire le comportement des matériaux avant même leur synthèse, économisant du temps et des ressources dans la recherche et développement.
Ces études peuvent être consultées sur des plateformes de publications scientifiques comme consultez les études de la théorie des bandes sur arXiv, où des articles de recherche sont librement accessibles.
















