Le modèle atomique de Bohr (1913) est une étape marquante dans la création de la mécanique quantique. Dans le modèle de l'atome établi par Rutherford, celui-ci est constitué d'électrons tournant autour d'un noyau chargé, composé de protons. L'ensemble est décrit par les équations de la mécanique de Newtonmécanique de Newton et celles de la théorie des électrons de Maxwell-Lorentz.
Il existait alors une contradiction fondamentale. D'après ces équations, un électron en orbiteorbite autour du noyau devait se mettre à rayonner et à perdre son énergieénergie. L'électron devait donc spiraler en direction du noyau, tout en émettant de la lumièrelumière composée d'un spectrespectre continu de longueurs d'ondeslongueurs d'ondes.
De plus, rien ne stabilisant l'orbite des électrons, les différents chocs des atomes d'un gazgaz entre eux devaient rapidement détruire ces orbites.
La théorie échouait donc à reproduire deux faits expérimentalement observés :
- l'existence même des atomes ;
- l'existence établie par la spectroscopie d'un spectre discret de longueurs d'ondes dans le rayonnement que les atomes sont capables d'émettre et d'absorber.
Dans ce dernier cas, une formule très curieuse avait pu être établie. Entre deux fréquencesfréquences et
, caractérisant des raies dans le spectre de l'atome d’hydrogène, existait lorsqu'on faisait leur soustraction la formule de Balmerformule de Balmer suivante :
n et m étant des entiers non nuls, la constante de Rydberg, et c la vitesse de la lumièrevitesse de la lumière.
Tout se passait donc comme s'il y avait des états d'énergie dans l'atome, ne pouvant varier que de façon discrète lors de l'émissionémission ou de l'absorptionabsorption de la lumière à une fréquence . Les raies étaient donc associées à des énergies
telles que :
Où est une constante qu'on définira plus loin.
Les spectres sont comme les papillons, pense le physicien danois Niels Bohr en ce début 1913. Les couleurs sont très belles, mais on a fait le tour du problème : grâce au spectroscope à prisme mis au point 50 ans plus tôt par les physiciens allemands Kirchhoff et Bunsen, tous les éléments chimiques ont fourni leur identité sous la forme de raies caractéristiques. Pourtant ce sont ces traits lumineux qui vont offrir à Bohr la clé du secret des atomes. © Synchrotron SOLEIL
Cela frappa Niels BohrNiels Bohr qui se rappela du résultat de Max PlanckMax Planck à propos de la formule du rayonnement du corps noir. En 1900, Planck avait en effet montré que l'on pouvait déduire le spectre du rayonnement d'un corps à l'équilibre thermique. On le pouvait en adoptant comme hypothèse que la matièrematière ne pouvait absorber ou émettre de la lumière que par paquetspaquets d'énergie à une fréquence donnée. Il avait énoncé une des plus fameuses formules de la physiquephysique avec
, elle s'écrivait
où
est la célèbre constante de Planckconstante de Planck.
Bohr reprit l’hypothèse de Planck
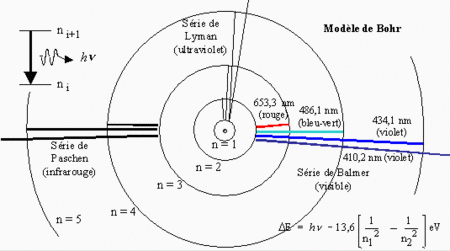
Bohr se servit de l'hypothèse de Planck pour postuler que les électrons dans le modèle de l'atome de Rutherford ne pouvaient circuler que sur des orbites quantifiées d'énergie . En sautant d'une orbite à une autre l'électron pouvait émettre un paquet d'énergie lumineuse discret, un photonphoton, dont la fréquence était donnée par :
D'après la théorie du rayonnement classique, la fréquence d'émission d'un rayonnement pour une particule chargée en orbite circulaire devait être l'inverse de sa période de révolutionpériode de révolution. On pouvait donc déterminer la taille d'un atome d'hydrogènehydrogène et calculer la constante à partir de la massemasse de l'électron, sa charge et de la constante de Planck
. Un résultat qui éblouit tout le monde.
L'état d'un atome d'hydrogène pouvait donc être décrit par l'introduction de nombres entiers n et m que l'on appellera « nombres quantiquesnombres quantiques principaux ». Des formules similaires seront obtenues pour des moléculesmolécules diatomiques modélisées par des haltères en rotation et surtout pour des atomes dits hydrogénoïdes.
Ce que l'on allait appeler dorénavant le modèle de Bohr de l'atome présente quelques caractéristiques fortes importantes qui se trouveront être déterminantes pour la découverte des principes de la mécanique quantique.
- D'abord, il explique et respecte le principe de combinaison de Ritz du nom de son découvreur. Si l'on considère des fréquences de raies spectralesraies spectrales pour l'atome d'hydrogène, des sommes ou des soustractions de ces fréquences donnent encore une raie spectrale possible de l'atome. C'est évident si l'on considère la formule de Balmer.
Prenons une transition avec émission d'un photon et
,
,
,
,
alors
=
+
=
+
=
+
+
avec émission de deux et trois photons.
- Ensuite, l'image spatio-temporelle du mouvementmouvement de l'électron lorsqu'il passe d'un niveau d'énergie à un autre est plus que problématique. S'il possédait une trajectoire intermédiaire entre deux orbites, pourquoi ne rayonne-t-il pas à ce moment-là en contradiction avec les lois de l'électrodynamique des particules chargées ? On est conduit à l'image d'un saut instantané d'une orbite à une autre sans localisation spatiale intermédiaire. Tout le schéma des principes physiques et des équations de la physique classique est ébranlé.
- Enfin, lorsque l'on considère la limite des transitions entre des niveaux d'énergies caractérisés par des grands nombres quantiques, disons n et n+1, la formule de Balmer donne un spectre qui se rapproche d'un spectre continu. En effet, on obtient :
Ce qui lorsque n devient très grand tend vers :
Ce qui correspond bien à une différence de plus en plus petite entre les fréquences d'émission et d'absorption de la lumière pour un électron sur ces orbites hautes.
Ceci est à l'origine du principe de correspondance de Bohrprincipe de correspondance de Bohr stipulant qu'à la limite des grands nombres quantiques caractérisant les systèmes atomiques on doit retrouver les formules de la physique classique. Ce principe permettra en particulier de connecter les formules donnant les intensités du rayonnement des atomes quantiques avec les formules classiques et donc guidera les théoriciens vers l'interprétation des équations quantiques en les connectant vers leurs limites classiques.
Ces trois caractéristiques seront de la plus haute importance pour la découverte par Heisenberg d'une mécanique matricielle des phénomènes quantiques.